Capítulo 1: El modelo de Ingreso-Gasto Keynesiano
Contents
Capítulo 1: El modelo de Ingreso-Gasto Keynesiano#
PARTE 1: Lectura de Dancourt, O. (2017). The lean times in the Peruvian economy. Journal of Post Keynesian Economics, 40(1), 112-129.#
El objetivo del artículo es presentar al choque externo adverso sufrido por la economía peruana como un suceso macroeconómico que continúa imapactando en el país. Es decir, el autor pretende; en primer lugar, describir el choque externo adverso sufrido por la economía peruana y su impacto recesivo durante 2014-15. En segundo lugar, analiza el impacto inflacionario de este choque externo. Después, describe las políticas monetarias y fiscales aplicadas en respuesta al choque externo. Y, finalmente, explora los retos macroeconómicos del nuevo gobierno de Pedro Pablo Kuczynski.
Para lograr su objetivo, describe con precisión el choque externo adverso, identificando dos causas para este enfriamiento de la economía urbana: 1.Ha estado asociado a una notable caída del valor de las exportaciones. y 2.Ha estado causado por una restricción crediticia en dólares. Por lo tanto, permite comprender que la paralización económica fue producto del desplome mundial de los precios de metales (que trajo consigo la reducción de los ingresos fiscales) y la sequía crediticia (que reduce el gasto privado y produce impulsos recesivos).
Bajo esta misma línea, pareciera que el autor intenta responder ¿Qué pasa con los choques externos adversos? ¿Cuáles son sus impactos?. Para ello aborda los conceptos de inflación y tipo de cambio, para los cuales argumenta que los choques adversos deterioran la balanza de pagos ocasionando un cambio en el alza de tipo de cambio, y; por lo tanto, eleva la inflación. Para esbozar esto, un punto fuerte es que presenta gráficos que ayudan a entender este comportamiento del tipo de cambio. Sin embargo, suele tener palabras teóricas de carácter económico con las que todavía resulta difícil de familiarizarse.
El autor también aborda lo que es la política monetaria y fiscal en el 2013-2015. En este punto, realiza una comparación válida entre “Lo que deben hacer las autoridades ante un choque externo adverso” vs. “Lo que realmente hicieron en materia de política monetaria y fiscal en el periodo 2013-2015”. Esta comparación resulta muy interesante para el análisis central que hacen. Sin embargo, puede ser visto como un punto débil en tanto se limita a suponer o establecer parámetros que hubieran podido resultar en un mejor descenlace “hipotéticamente”.
Finalmente, para responder a su objetivo de estudio, Durand plantea los desafíos a los que el nuevo gobierno se verá sometido tras el impacto del choque adverso. Hace un balance de los aspectos que hereda el gobierno (paralización económica, inflación y déficit fiscal alyo) y sus nuevas tareas (resctivación productiva, impulso monetario, impulso fiscal, diversificación económica). Este análisis final adquiere un gran valor para reflexionar acerca de que el estancamiento económico en el país continuará si el nuevo gobierno continúa con las prácticas monetarias y fiscales que se dieron entre el 2014-2015.
Un próximo paso para avanzar en este análisis sería la lectura de nuevos artículos posteriores al gobierno de PPK, donde se pueda examinar las decisiones monetarias y fiscales que se han abordado para analizar si el estancamiento económico en relación a las políticas de 2014-2015 sigue perpetuando (Lectura recomendada: https://www.scielo.cl/pdf/revcipol/v40n2/0718-090X-revcipol-S0718-090X2020005000116.pdf). Otra variable a considerar para el análisis será el impacto que ha traído consigo el covid-19 para la economía peruana (Artículo recomendado: https://cooperaccion.org.pe/wp-content/uploads/2020/07/final-28-junio-POLITICA-FISCAL-Y-RECUPERACION-EN-PANDEMIA-1.pdf). Para finalizar, sería muy beneficioso poder explorar otros casos similares al de Perú en la región y evaluar las salidas y las decisiones monetarias y fiscales que tomaron (Lectura recomendada: https://www.kas.de/c/document_library/get_file?uuid=22b68ade-3969-4b71-243b-216ab094bbf9&groupId=252038).
PARTE 2: Código en Python#
Derive y explique la función de demanda de Consumo.#
Considerando, en primer lugar que la tributación está dada por:
(Donde “t” está dada por la tributación promedio)
Entonces, el ingreso neto de tributación es el Ingreso Disponible (suponiendo que las transferencias son iguales a 0)
Este ingreso disponible será empleado en los gastos de consumo, siendo:
“\( C_0 \)” representa el nivel básico de consumo (Consumo autónomo) y “b” es el cambio en el consumo por unidad de cambio en el ingreso disponible. Esto será la Propensión Marginal a Consumir \( PM_gC \)
\( PM_gC \) será la derivada de la función consumo con respecto al ingreso disponible:
$\( \frac{dC}{dY^d}\ = b \)$ donde (0<b<1)
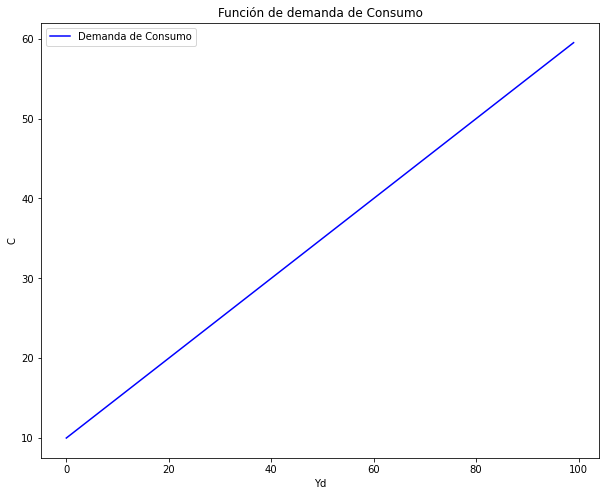
Ahora, Grafiquemos la Función de demanda de Consumo:
Tenemos que según la PMgC “b” = 0.5
La función de consumo será $\( C = 10 + 0.5{Y^d} \)$
# Se cargan las librerías
import ipywidgets as widgets
import matplotlib.pyplot as plt
import numpy as np
import sympy as sy
from sympy import *
import pandas as pd
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Input In [1], in <cell line: 8>()
6 import sympy as sy
7 from sympy import *
----> 8 import pandas as pd
File ~\anaconda3\lib\site-packages\pandas\__init__.py:48, in <module>
45 # let init-time option registration happen
46 import pandas.core.config_init
---> 48 from pandas.core.api import (
49 # dtype
50 Int8Dtype,
51 Int16Dtype,
52 Int32Dtype,
53 Int64Dtype,
54 UInt8Dtype,
55 UInt16Dtype,
56 UInt32Dtype,
57 UInt64Dtype,
58 Float32Dtype,
59 Float64Dtype,
60 CategoricalDtype,
61 PeriodDtype,
62 IntervalDtype,
63 DatetimeTZDtype,
64 StringDtype,
65 BooleanDtype,
66 # missing
67 NA,
68 isna,
69 isnull,
70 notna,
71 notnull,
72 # indexes
73 Index,
74 CategoricalIndex,
75 RangeIndex,
76 MultiIndex,
77 IntervalIndex,
78 TimedeltaIndex,
79 DatetimeIndex,
80 PeriodIndex,
81 IndexSlice,
82 # tseries
83 NaT,
84 Period,
85 period_range,
86 Timedelta,
87 timedelta_range,
88 Timestamp,
89 date_range,
90 bdate_range,
91 Interval,
92 interval_range,
93 DateOffset,
94 # conversion
95 to_numeric,
96 to_datetime,
97 to_timedelta,
98 # misc
99 Flags,
100 Grouper,
101 factorize,
102 unique,
103 value_counts,
104 NamedAgg,
105 array,
106 Categorical,
107 set_eng_float_format,
108 Series,
109 DataFrame,
110 )
112 from pandas.core.arrays.sparse import SparseDtype
114 from pandas.tseries.api import infer_freq
File ~\anaconda3\lib\site-packages\pandas\core\api.py:29, in <module>
17 from pandas.core.dtypes.missing import (
18 isna,
19 isnull,
20 notna,
21 notnull,
22 )
24 from pandas.core.algorithms import (
25 factorize,
26 unique,
27 value_counts,
28 )
---> 29 from pandas.core.arrays import Categorical
30 from pandas.core.arrays.boolean import BooleanDtype
31 from pandas.core.arrays.floating import (
32 Float32Dtype,
33 Float64Dtype,
34 )
File ~\anaconda3\lib\site-packages\pandas\core\arrays\__init__.py:6, in <module>
1 from pandas.core.arrays.base import (
2 ExtensionArray,
3 ExtensionOpsMixin,
4 ExtensionScalarOpsMixin,
5 )
----> 6 from pandas.core.arrays.boolean import BooleanArray
7 from pandas.core.arrays.categorical import Categorical
8 from pandas.core.arrays.datetimes import DatetimeArray
File <frozen importlib._bootstrap>:1007, in _find_and_load(name, import_)
File <frozen importlib._bootstrap>:986, in _find_and_load_unlocked(name, import_)
File <frozen importlib._bootstrap>:680, in _load_unlocked(spec)
File <frozen importlib._bootstrap_external>:846, in exec_module(self, module)
File <frozen importlib._bootstrap_external>:941, in get_code(self, fullname)
File <frozen importlib._bootstrap_external>:1039, in get_data(self, path)
KeyboardInterrupt:
Yd_size = 100 #tamaño
#Parámetros de las variables
Co=10
b=0.5
#Creamos valores para Yd:
Yd = np.arange(Yd_size)
#Traemos la ecuación de consumo:
def C(Co, b, Yd):
C = Co + (b*Yd)
return C
C = C(Co, b, Yd)
C
array([10. , 10.5, 11. , 11.5, 12. , 12.5, 13. , 13.5, 14. , 14.5, 15. ,
15.5, 16. , 16.5, 17. , 17.5, 18. , 18.5, 19. , 19.5, 20. , 20.5,
21. , 21.5, 22. , 22.5, 23. , 23.5, 24. , 24.5, 25. , 25.5, 26. ,
26.5, 27. , 27.5, 28. , 28.5, 29. , 29.5, 30. , 30.5, 31. , 31.5,
32. , 32.5, 33. , 33.5, 34. , 34.5, 35. , 35.5, 36. , 36.5, 37. ,
37.5, 38. , 38.5, 39. , 39.5, 40. , 40.5, 41. , 41.5, 42. , 42.5,
43. , 43.5, 44. , 44.5, 45. , 45.5, 46. , 46.5, 47. , 47.5, 48. ,
48.5, 49. , 49.5, 50. , 50.5, 51. , 51.5, 52. , 52.5, 53. , 53.5,
54. , 54.5, 55. , 55.5, 56. , 56.5, 57. , 57.5, 58. , 58.5, 59. ,
59.5])
Empezamos graficando:
#dimensionando el gráfico
y_max = np.max(C)
fig, ax = plt.subplots(figsize=(10, 8))
#curva Demanda de consumo
ax.plot(Yd, C, label = "Demanda de Consumo", color = "blue")
#leyenda y título
ax.set(title="Función de demanda de Consumo", xlabel= r'Yd', ylabel= r'C')
ax.legend()
<matplotlib.legend.Legend at 0x28484f9afd0>
Derive y explique la función de Inversión.#
La función de Inversión está dada por $\( I = {I_0} - hr \)$
Donde el Gasto en inversió (I) representa a los gastos que hacen que incremente el stock de capital, y la producción a largo plazo. Aquí se incluyen los conceptos de inversión bruta fija y de variación de existencias de las empresas.
“I” dependerá de la tasa de interés real (r) y de la inversión autónoma (Io) que está dada por los inversionistas.
Replicando la gráfica de función de demanda de Inversión
r_size=100 #definiendo tamaño para r
r = np.arange(r_size)
r
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
#Parametrando
Io= 55
h= 0.5
#Función de inversión
def I(Io, h, r):
I = Io-(h*r)
return I
I = Io-(h*r)
I
array([55. , 54.5, 54. , 53.5, 53. , 52.5, 52. , 51.5, 51. , 50.5, 50. ,
49.5, 49. , 48.5, 48. , 47.5, 47. , 46.5, 46. , 45.5, 45. , 44.5,
44. , 43.5, 43. , 42.5, 42. , 41.5, 41. , 40.5, 40. , 39.5, 39. ,
38.5, 38. , 37.5, 37. , 36.5, 36. , 35.5, 35. , 34.5, 34. , 33.5,
33. , 32.5, 32. , 31.5, 31. , 30.5, 30. , 29.5, 29. , 28.5, 28. ,
27.5, 27. , 26.5, 26. , 25.5, 25. , 24.5, 24. , 23.5, 23. , 22.5,
22. , 21.5, 21. , 20.5, 20. , 19.5, 19. , 18.5, 18. , 17.5, 17. ,
16.5, 16. , 15.5, 15. , 14.5, 14. , 13.5, 13. , 12.5, 12. , 11.5,
11. , 10.5, 10. , 9.5, 9. , 8.5, 8. , 7.5, 7. , 6.5, 6. ,
5.5])
Gráfico demanda de Inversión
# Dimensiones
y_max = np.max(I)
fig, ax = plt.subplots(figsize=(10, 8))
# Curva
ax.plot(r, I, label = "Demanda de Inversion", color = "Green")
# Leyenda y título
ax.set(title="Función demanda de Inversión", xlabel= r'r', ylabel= r'I')
ax.legend()
<matplotlib.legend.Legend at 0x28483b38430>

¿Cuáles son los supuestos del modelo Ingreso-Gasto Keynesiano?.#
El modelo Ingreo-Gasto Keynesiano (cruz keynesiana) está dado por tres supuestos:
El modelo supone que el nivel de precios está fijo. (precios rígidos)
El nivel del producto se adapta a los cambios en la demanda agregada.
La tasa de interés está determinada fuera del modelo (en el mercado monetario).
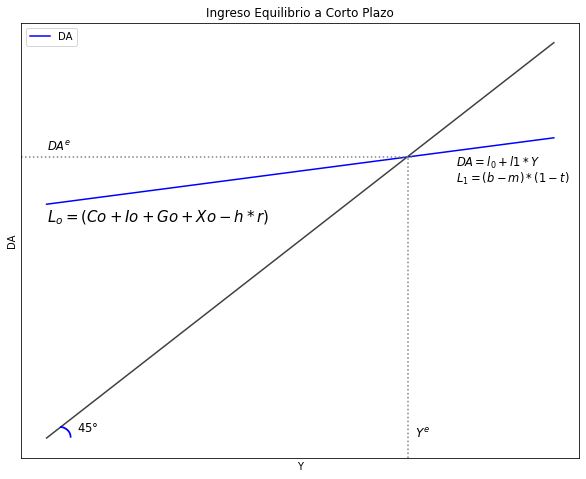
A partir de las ecuaciones de Ingreso-Gasto y la función de Demanda Agregada:#
Encuentre el nivel de Ingreso de equilibrio de \( {Y^e} \)
Ecuación de la Demanda Agregada:
Por lo tanto:
El punto de quilibrio –> estará dado por DA = Y
Ahora, la ecuación de nivel de ingreso de equilibrio estará observada por: $\( Y = ({C_0}+{I_0}+{G_0}+{X_0}-hr)+(b-m)(1-t)Y \)\( \)\( Y = \frac{1}{1-(b-m)(1-t)}{C_0}+{I_0}+{G_0}+{X_0}-hr \)$
Replique el siguiente gráfico con todas las descripciones encima de las rectas.
Y_size = 100
#Parametrando
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
r = 0.9
b = 0.8
m = 0.2
t = 0.3
Y = np.arange(Y_size)
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
# Recta 45°
a = 2.5
def L_45(a, Y):
L_45 = a*Y
return L_45
L_45 = L_45(a, Y)
#Graficando
# Dimensiones
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas
ax.plot(Y, DA_IS_K, label = "DA", color = "#0000ff") #Demanda agregada
ax.plot(Y, L_45, color = "#404040") #Línea de 45º
# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
# Líneas punteadas punto de equilibrio
plt.axvline(x=70.5, ymin= 0, ymax= 0.69, linestyle = ":", color = "grey")
plt.axhline(y=176, xmin= 0, xmax= 0.7, linestyle = ":", color = "grey")
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(80, 170, '$DA=l_0+l1*Y$', fontsize = 11.5, color = 'black')
plt.text(80, 160, '$L_1=(b - m)*(1 - t)$', fontsize = 11.5, color = 'black')
plt.text(72, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(0, 135, '$L_o=(Co + Io + Go + Xo - h*r)$', fontsize = 15, color = 'black')
# línea 45º
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = 'Blue')
# Título y leyenda
ax.set(title="Ingreso Equilibrio a Corto Plazo", xlabel= r'Y', ylabel= r'DA')
ax.legend()
plt.show()
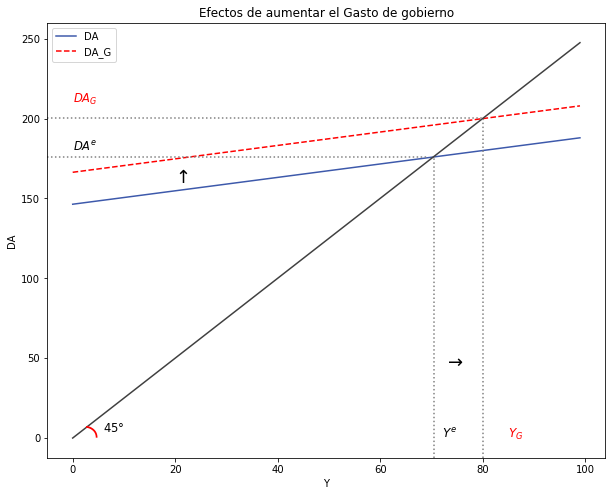
Estática comparativa en el modelo de Ingreso-Gasto keynesiano:#
Analice una Política Fiscal Expansiva con aumento del Gasto del Gobierno. El análisis debe ser intuitivo, matemático y gráfico.
–> Intuición:
–> Matemáticamente:
considerando el multiplicador keynesiano, k>0:
si no se observan cambios en Co, Io, Xo, h ni r, entonces:
Sabiendo que \(ΔG_0\) > 0 y que k > 0, la multiplicación de un número negativo con un positivo dará otro negativo:
–> Gráficamente:
#Parametrando Curva de ingreso de equilibriio Original
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Ecuación
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
#--------------------------------------------------
# NUEVA curva de ingreso de equilibrio
#Parámetro cambiado
Go = 90
# Generando ecuación con el nuevo parámetro
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_G = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
#Dimensiones del grafico
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, DA_IS_K, label = "DA", color = "#3D59AB") #curva ORIGINAL
ax.plot(Y, DA_G, label = "DA_G", color = "red", linestyle = 'dashed') #NUEVA curva
ax.plot(Y, L_45, color = "#404040") #línea de 45º
# Lineas punteadas
plt.axvline(x = 70.5, ymin= 0, ymax = 0.69, linestyle = ":", color = "grey")
plt.axhline(y = 176, xmin= 0, xmax = 0.68, linestyle = ":", color = "grey")
plt.axvline(x = 80, ymin= 0, ymax = 0.78, linestyle = ":", color = "grey")
plt.axhline(y = 200.5, xmin= 0, xmax = 0.78, linestyle = ":", color = "grey")
# Texto agregado
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(0, 210, '$DA_G$', fontsize = 11.5, color = 'red')
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = 'red')
plt.text(72, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(85, 0, '$Y_G$', fontsize = 12, color = 'red')
plt.text(73, 45, '$→$', fontsize = 18, color = 'black')
plt.text(20, 160, '$↑$', fontsize = 18, color = 'black')
# Título y leyenda
ax.set(title = "Efectos de aumentar el Gasto de gobierno", xlabel = r'Y', ylabel = r'DA')
ax.legend()
plt.show()
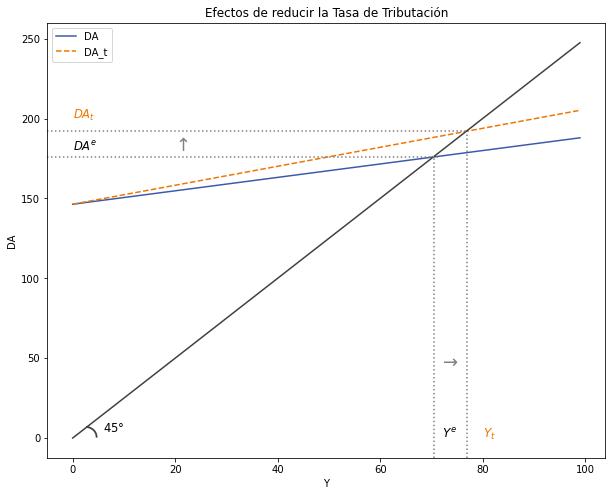
Analice una Política Fiscal Expansiva con una reducción de la Tasa de Tributación. El análisis debe ser intuitivo, matemático y gráfico.
–> Intuición:
–> Matemáticamente: Δt<𝑂→¿Δ𝑌?
Co, Io, Go, Xo, h, r, b, m, t = symbols('Co Io Go Xo h r b m t')
f = (Co + Io + Go + Xo - h*r)/(1-(b-m)*(1-t))
df_t = diff(f, t)
df_t #∆Y/∆t
Considernado el diferencial de Δt:
Sabiendo que b > m, entonces \((m-b) < 0\)
Los componentes autónomos no cambian: \(∆C_0 = ∆I_0 = ∆X_0 = ∆h = ∆r = 0\)
Cualquier número elevado al cuadrado será positivo: \( (1-(1-t)(b-m)+1)^2 > 0 \)
Entonces:
Dado que \(∆t < 0\), la división de dos positivos da otro positivo:
–> Gráficamente:
# Curva de ingreso de equilibrio ORIGINAL
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3 #tasa de tributación
r = 0.9
Y = np.arange(Y_size)
# Ecuación
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
# NUEVA curva de ingreso de equilibrio
# Definir SOLO el parámetro cambiado
t = 0.01
# Generar la ecuación con el nuevo parámetros
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_t = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
# Gráfico
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, DA_IS_K, label = "DA", color = "#3D59AB") #curva ORIGINAL
ax.plot(Y, DA_t, label = "DA_t", color = "#EE7600", linestyle = 'dashed') #NUEVA curva
ax.plot(Y, L_45, color = "#404040") #línea de 45º
# Lineas punteadas
plt.axvline(x = 70.5, ymin= 0, ymax = 0.69, linestyle = ":", color = "grey")
plt.axhline(y = 176, xmin= 0, xmax = 0.7, linestyle = ":", color = "grey")
plt.axvline(x = 77, ymin= 0, ymax = 0.75, linestyle = ":", color = "grey")
plt.axhline(y = 192, xmin= 0, xmax = 0.75, linestyle = ":", color = "grey")
# Texto agregado
plt.text(0, 180, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(0, 200, '$DA_t$', fontsize = 11.5, color = '#EE7600')
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
plt.text(72, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(80, 0, '$Y_t$', fontsize = 12, color = '#EE7600')
plt.text(72, 45, '$→$', fontsize = 18, color = 'grey')
plt.text(20, 180, '$↑$', fontsize = 18, color = 'grey')
# Título y leyenda
ax.set(title = "Efectos de reducir la Tasa de Tributación", xlabel = r'Y', ylabel = r'DA')
ax.legend()
plt.show()
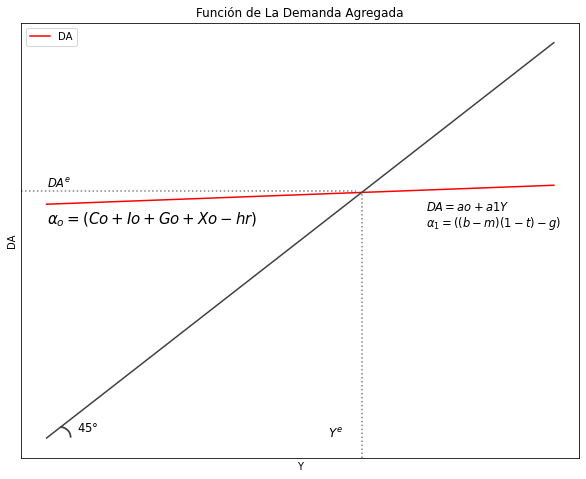
Estática comparativa en el modelo de Ingreso-Gasto keynesiano con Regla Contracíclica.#
Grafique la Funcion de demanda Agregada y la recta de 45 grados señalando los valores de intercepto y pendiente como en el apartado
# Parametramdo
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
g = 0.3
Y = np.arange(Y_size)
# Ecuación de la curva del ingreso de equilibrio
def DA_g(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_g = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)-g)*Y
return DA_g
DA_IS_G = DA_g(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# Graficando
# Dimensiones del gráfico
y_max = np.max(DA_IS_G)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, DA_IS_G, label = "DA", color = "red") #Demanda agregada
ax.plot(Y, L_45, color = "#404040") #Línea de 45º
# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
# Líneas punteadas punto de equilibrio
plt.axvline(x=61.5, ymin= 0, ymax= 0.61, linestyle = ":", color = "grey")
plt.axhline(y=154.5, xmin= 0, xmax= 0.60, linestyle = ":", color = "grey")
# Texto agregado
# punto de equilibrio
plt.text(0, 157, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(74, 142, '$DA = ao + a1Y$', fontsize = 11.5, color = 'black')
plt.text(74, 132, '$α_1=((b - m)(1 - t)-g)$', fontsize = 11.5, color = 'black')
plt.text(55, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(0, 134, '$α_o=(Co + Io + Go + Xo - hr)$', fontsize = 15, color = 'black')
# línea 45º
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
# Título y leyenda
ax.set(title="Función de La Demanda Agregada", xlabel= r'Y', ylabel= r'DA')
ax.legend() #mostrar leyenda
plt.show()
Encuentre el nivel de Ingreso de equilibrio
Conociendo la ecuación de la demanda agregada:
DA=L0+L1Y
El punto de quilibrio –> estará dado por DA = Y
Ahora, la ecuación de condición de equilibrio estará observada por: $\( Y = ({C_0}+{I_0}+{G_0}+{X_0}-hr)+((b-m)(1-t)-g)Y \)\( \)\( Y = \frac{1}{1-(b-m)(1-t)+g}{C_0}+{I_0}+{G_0}+{X_0}-hr \)$
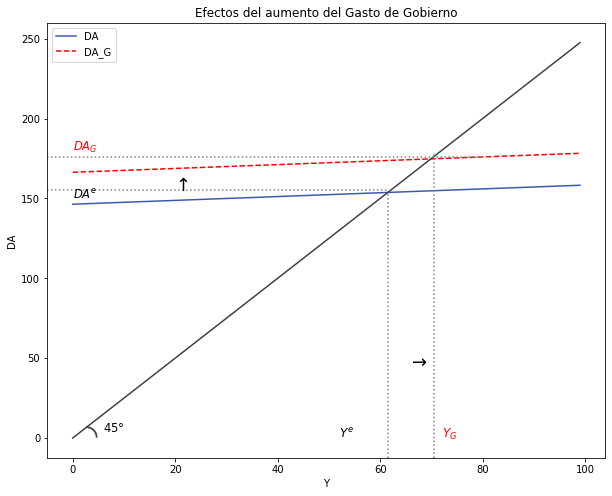
Analice una Política Fiscal Expansiva con aumento del Gasto del Gobierno. El análisis debe ser intuitivo, matemático y gráfico.
–> Intuición:
–> Matemáticamente: ΔGo > 0 → ¿Δ𝑌?
considerando k
\( ∆Y= k(∆C_0 + ∆I_0 + ∆G_0 + ∆X_0 - ∆h - ∆r \)
Si no se encuentran cambios en Co, Io, X0, h o r entonces:
\( ∆C_0= ∆I_0 = ∆X_0 = ∆h = ∆r = 0\) \( ∆Y= k(∆G_0) \)
\( ∆Y=(+)(+) \) \( ∆Y > 0 \)
Graficando
# Curva de ingreso de equilibrio ORIGINAL
# Parametrandoo
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
g = 0.3
Y = np.arange(Y_size)
# Ecuación
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)-g)*Y
return DA_K
DA_IS_G = DA_K(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# NUEVA curva de ingreso de equilibrio
Go = 90
# Generar la ecuación con el nuevo parámetro
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)-g)*Y
return DA_K
DA_GG = DA_K(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# Gráfico
#Dimensiones del grafico
y_max = np.max(DA_IS_G)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, DA_IS_G, label = "DA", color = "#3D59AB") #curva ORIGINAL
ax.plot(Y, DA_GG, label = "DA_G", color = "red", linestyle = 'dashed') #NUEVA curva
ax.plot(Y, L_45, color = "#404040") #línea de 45º
# Lineas punteadas
plt.axvline(x = 61.5, ymin= 0, ymax = 0.61, linestyle = ":", color = "grey")
plt.axhline(y = 155, xmin= 0, xmax = 0.61, linestyle = ":", color = "grey")
plt.axvline(x = 70.5, ymin= 0, ymax = 0.70, linestyle = ":", color = "grey")
plt.axhline(y = 176, xmin= 0, xmax = 0.78, linestyle = ":", color = "grey")
# Texto agregado
plt.text(0, 150, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(0, 180, '$DA_G$', fontsize = 11.5, color = 'red')
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
plt.text(52, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(72, 0, '$Y_G$', fontsize = 12, color = 'red')
plt.text(66, 45, '$→$', fontsize = 18, color = 'black')
plt.text(20, 155, '$↑$', fontsize = 18, color = 'black')
# Título y leyenda
ax.set(title = "Efectos del aumento del Gasto de Gobierno", xlabel = r'Y', ylabel = r'DA')
ax.legend()
plt.show()
¿Cuál es el papel que juega el parametro en el multiplicador keynesiano?
G generará un aumento del ingreso y, a su vez en la tasa de interés. Según el modelo-gasto kenyesiano. Reduciendo el tamaño del multiplicador.
El tamaño del efecto de la política fiscal encontrado en 6 es el mismo que en el apartado 5 ?
Tanto en el apartado 5 como en el 6, el gasto se presenta en la misma cantidad. Empero, esto no significa que el efecto para ambos modelos sea el mismo. La teoría muestra que en un modelo de política fiscal contracíclica la pendiente de la Demanda Agregada es menor.
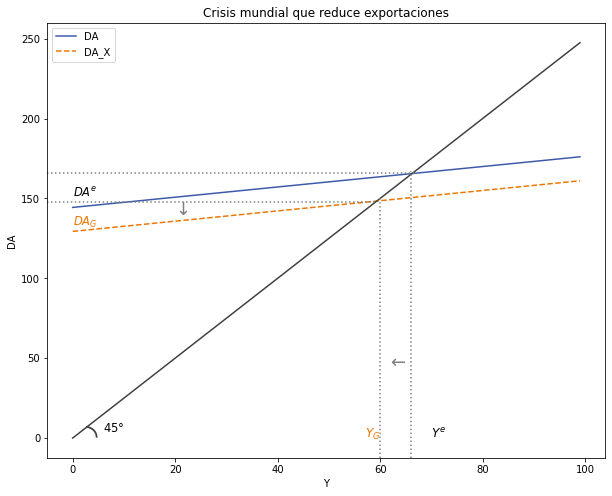
Analice una crisis mundial que reduce nuestras exportaciones. El análisis debe ser intuitivo, matemático y gráfico.#
Intuitivamente
Matemáticamente
Gráficamente
#--------------------------------------------------
# Curva de ingreso de equilibrio ORIGINAL
# Parametrando
Y_size = 100
Co = 35
Io = 40
Go = 50
Xo = 20
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
g = 0.1
Y = np.arange(Y_size)
# Ecuación
def DA_IS_K(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_IS_K = (Co + Io + Go + Xo - h*r) + (((b - m)*(1 - t)-g)*Y)
return DA_IS_K
DA_IS_K = DA_IS_K(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
#--------------------------------------------------
# NUEVA curva de ingreso de equilibrio con reducción de exportaciones
Xo = 5
def DA_X(Co, Io, Go, Xo, h, r, b, m, t, g, Y):
DA_X = (Co + Io + Go + Xo - h*r) + (((b - m)*(1 - t)-g)*Y)
return DA_X
DA_X = DA_X(Co, Io, Go, Xo, h, r, b, m, t, g, Y)
# Gráfico
y_max = np.max(DA_IS_K)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, DA_IS_K, label = "DA", color = "#3D59AB") #curva ORIGINAL
ax.plot(Y, DA_X, label = "DA_X", color = "#EE7600", linestyle = 'dashed') #curva NUEVA
ax.plot(Y, L_45, color = "#404040") #línea de 45º
# Lineas punteadas
plt.axvline(x = 66, ymin= 0, ymax = 0.66, linestyle = ":", color = "grey")
plt.axhline(y = 166, xmin= 0, xmax = 0.66, linestyle = ":", color = "grey")
plt.axvline(x = 60, ymin= 0, ymax = 0.60, linestyle = ":", color = "grey")
plt.axhline(y = 148, xmin= 0, xmax = 0.59, linestyle = ":", color = "grey")
# Texto agregado
plt.text(0, 151, '$DA^e$', fontsize = 11.5, color = 'black')
plt.text(0, 133, '$DA_G$', fontsize = 11.5, color = '#EE7600')
plt.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
plt.text(2.5, -3, '$◝$', fontsize = 30, color = '#404040')
plt.text(57, 0, '$Y_G$', fontsize = 12, color = '#EE7600')
plt.text(70, 0, '$Y^e$', fontsize = 12, color = 'black')
plt.text(62, 45, '$←$', fontsize = 18, color = 'grey')
plt.text(20, 140, '$↓$', fontsize = 18, color = 'grey')
# Título y leyenda
ax.set(title = "Crisis mundial que reduce exportaciones", xlabel = r'Y', ylabel = r'DA')
ax.legend()
plt.show()