Capítulo 5: El Modelo DA-OA

PARTE 1: Lectura de Dancourt, Oscar. (2014). Metas de inflación en Perú: las razones del éxito

Dancourt en su texto “Inflation Targeting in Peru: The Reasons for the Success” parte por la formulación del problemático contexto de los 2000, donde el Banco Central Peruano decide adoptar dos nuevas decisiones para lograr la estabilidad financiera. Estas dos decisiones consistían en implementar un sistema de objetivos de inflación y acumular las suficientes reservas de divisas. A partir de esto, el autor se plantea analizar el impacto de estos instrumentos de política monetaria durante el periodo de 2002-2013 y, a su vez, revisar el proceso de desdolarización del crédito bancario.

Para responder a lo anterior, Dancourt analiza en primer lugar, la etapa 2002-2013. El autor concluye que el buen desempeño macroeconómico que tuvo el país durante ese periodo no debe ser atribuido únicamente a la gestión de la política monetaria, pues el contexto externo se encontraba favorable. Este es un punto fuerte, pues Dancourt es objetivo con el análisis y aluce que el factor externo pudo haber influido favorablemente en la estabilidad económica. Para ser precisos, asegura que fueron los precios elevados de los bienes que se exportaban los que influyeron de manera directa en el comportamiento de los componentes de inversión, el gasto público y el tipo de cambio. Sin embargo, existen dos momentos excepcionales en donde el contexto externo no fue favorable: la crisis económica de 2008-2009 y la etapa del 2013 en la caída mundial de los precios de los metales.

Después de su análisis, Dancourt concluye que las lecciones de los sucesos del 2008-2009 son importantes, pues enseñan que el banco central debe reducir la tasa de interés y vender moneda extranjera en respuesta a shocks externos adversos. En segundo lugar, el banco central debe aumentar la tasa de interés y comprar divisas en respuesta a shocks externos favorables. Sin embargo, queda por ver si este esquema de política monetaria, que ha servido efectivamente durante la última década, puede proporcionar los mismos buenos resultados en un contexto externo desfavorable más prolongado. Y queda por ver si este régimen de política monetaria puede operar sin la tasa de interés de referencia como principal instrumento del banco central. Asimismo, Dancourt señala que para prevenir crisis bancarias, el banco central debe limitar el endeudamiento externo de los bancos comerciales (si no se hace esto sería imposible desdolarizar el crédito bancario). De esta manera, el único mecanismo efectivo es imponer requisitos de reserva más altos a la deuda externa de los bancos comerciales.

A pesar de que el documento presenta muchas fortalezas, una debilidad sería que si bien el autor menciona que el Banco Central toma ciertas medidas, no termina por explicar teóricamente los motivos por los que los BC optan por acumular o adquirir divisas. Otra limitación recae en que el esquema presentado por Dancourt no termina por convencer si puede ser útil a replicar en un contexto de crisis prolongada.

Finalmente, la problemática planteada por el autor puede ser profundizada a través del estudio de las políticas económicas usadas por el Banco Central del Perú para afrontar los años de crisis tras el COVID-19. De esta manera, se pudiera comparar el modelo planteado por el autor, con un suceso de crisis prolongado como lo viene siendo la pandemia. En esta misma línea, el aporte de Ortiz y Winkelried (2020) sobre “Hitos de la reforma macroeconómica en el Perú 1990-2020” es un buen punto de partida para este análisis. Asimismo, a partir del análisis del Reporte Inflacionario del BCR (2021) (recuadro 4), se puede abrir una línea de investigación sobre los efectos macroeconómicos a largo plazo del COVID-19.

PARTE 2: Código en Python -

Código hecho por Karen Arevalo y Mayeli Charra

A partir del siguiente sistema de ecuaciones que representan el modelo DA-OA

1. Encuentro con las ecuaciones de Ingreso (\( Y^e \)), tasa de interes (\( r^e \)), (\( P^e \)) de equilibrio (Escriba paso a paso la derivación de estas ecuaciones).

import numpy as np
import sympy as sy
from sympy import *
import pandas as pd
import matplotlib.pyplot as plt

Sabiendo que en el modelo DA-OA existen tres variables endógenas: \(Y^{eq} , r^{eq} , P^{eq}\)

Considerando la ecuación de la demanda agregada \((DA)\):

\[ P = \frac{h Mo^s + jB_o}{h} - \frac{jB_1 + hk}{h}Y ... (1)\]

Y la ecuación de la oferta agregada \((OA)\):

\[ P = P^e + θ(Y - \bar{Y}) ... (2)\]

• Para hallar \(Y^{eq-da-oa}\) igualamos ambas ecuaciones:

\[ \frac{h Mo^s + jB_o}{h} - \frac{jB_1 + hk}{h}Y = P^e + θ(Y - \bar{Y}) \]

\[ Y^{eq-da-oa} = (\frac{h Mo^s + jB_o}{h} - P^e + θ\bar{Y}) : (θ - \frac{jB_1 + hk}{h}) \]

• Para hallar \(P^{eq}\), despejamos la ecuación de \(OA\) en función de Y:

\[ P^{eq-da-oa} = P^{e} + θ(Y^{eq-da-oa} - \bar{Y}) \]

\[ Y = \frac{P - P^{eq} - θ\bar{Y}}{θ} \]

Y reemplazamos \(Y^{eq}\) en la ecuación de

\[ P^{eq-da-oa}= (\frac{h Mo^s + jB_o}{h} - \frac{jB_1 + hk}{h}) * (\frac{P - P^e - θ\bar{Y}}{θ}) \]

• Para encontrar \(r^{eq-da-oa}\) es necesario reemplazar \(P^{eq-da-oa}\) en la ecuación de tasa de interés de equilibrio del modelo IS-LM.

Tasa de interés de equilibrio:

\[ r^{eq-is-lm} = \frac{kB_0}{kh + jB_1} - (\frac{B_1}{kh + jB_1}) * (Ms_o - P) \]

Tasa de interés de equilibrio en DA-OA:

\[ r^{eq-is-lm} = \frac{kB_0}{kh + jB_1} - (\frac{B_1}{kh + jB_1}) * (Ms_o - P^{eq-da-oa}) \]

\( r^{eq-da-oa} = \frac{kB_0}{kh + jB_1} - (\frac{B_1}{kh + jB_1}) * (Ms_o - P^e + θ([\frac{1}{(θ + \frac{jB_1 + hk}{h})}] * [(\frac{hMo^s + jB_0}{h} - P^e + θ\bar{Y})] - \bar{Y})) \)

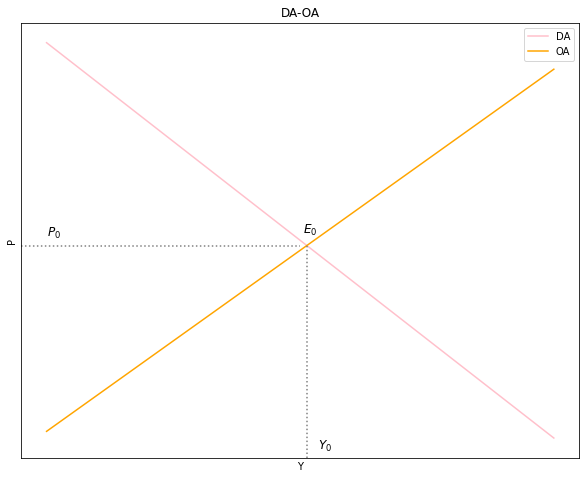
2. Grafique el equilibrio simultáneo en el modelo DA-OA.

#1--------------------------
    # Demanda Agregada
    
# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

k = 2
j = 1                
Ms = 200             
P  = 8  

Y = np.arange(Y_size)


# Ecuación

B0 = Co + Io + Go + Xo
B1 = 1 - (b-m)*(1-t)

def P_AD(h, Ms, j, B0, B1, k, Y):
    P_AD = ((h*Ms + j*B0)/h) - (Y*(j*B1 + h*k)/h)
    return P_AD

P_AD = P_AD(h, Ms, j, B0, B1, k, Y)


#2--------------------------
    # Oferta Agregada
    
# Parámetros

Y_size = 100

Pe = 100 
θ = 3
_Y = 20   

Y = np.arange(Y_size)


# Ecuación

def P_AS(Pe, _Y, Y, θ):
    P_AS = Pe + θ*(Y-_Y)
    return P_AS

P_AS = P_AS(Pe, _Y, Y, θ)

# líneas punteadas autómaticas

    # definir la función line_intersection
def line_intersection(line1, line2):
    xdiff = (line1[0][0] - line1[1][0], line2[0][0] - line2[1][0])
    ydiff = (line1[0][1] - line1[1][1], line2[0][1] - line2[1][1])

    def det(a, b):
        return a[0] * b[1] - a[1] * b[0]

    div = det(xdiff, ydiff)
    if div == 0:
       raise Exception('lines do not intersect')

    d = (det(*line1), det(*line2))
    x = det(d, xdiff) / div
    y = det(d, ydiff) / div
    return x, y

    # coordenadas de las curvas (x,y)
A = [P_AD[0], Y[0]] # DA, coordenada inicio
B = [P_AD[-1], Y[-1]] # DA, coordenada fin

C = [P_AS[0], Y[0]] # L_45, coordenada inicio
D = [P_AS[-1], Y[-1]] # L_45, coordenada fin

    # creación de intersección

intersec = line_intersection((A, B), (C, D))
intersec # (y,x)

(192.39043824701196, 50.79681274900399)

# Gráfico del modelo DA-OA

# Dimensiones del gráfico
y_max = np.max(P)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar 
ax.plot(Y, P_AD, label = "DA", color = "pink") #DA
ax.plot(Y, P_AS, label = "OA", color = "orange") #OA

# Líneas punteadas
plt.axhline(y=intersec[0], xmin= 0, xmax= 0.5, linestyle = ":", color = "grey")
plt.axvline(x=intersec[1],  ymin= 0, ymax= 0.49, linestyle = ":", color = "grey")

# Texto agregado
plt.text(0, 200, '$P_0$', fontsize = 12, color = 'black')
plt.text(53, 25, '$Y_0$', fontsize = 12, color = 'black')
plt.text(50, 202, '$E_0$', fontsize = 12, color = 'black')


# Eliminar valores de ejes
ax.yaxis.set_major_locator(plt.NullLocator())   
ax.xaxis.set_major_locator(plt.NullLocator())

# Título, ejes y leyenda
ax.set(title="DA-OA", xlabel= r'Y', ylabel= r'P')
ax.legend()

plt.show()

Estática comparativa

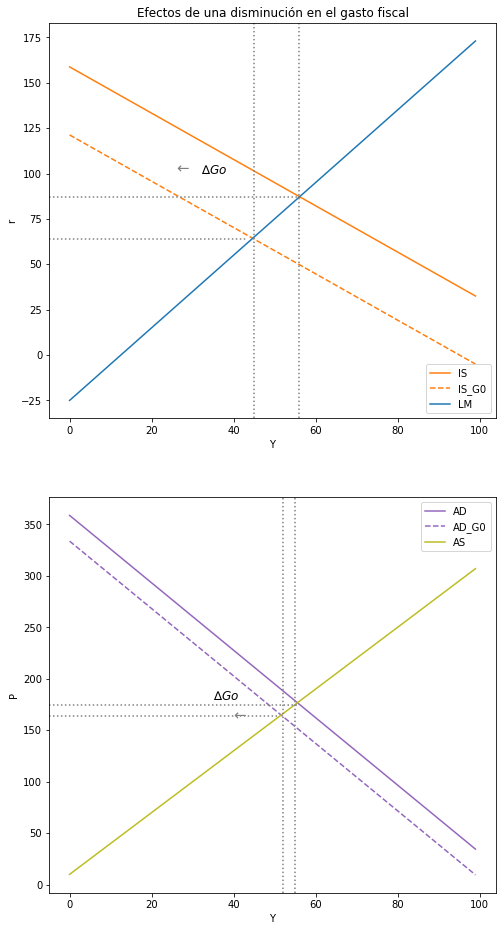
1. Analice los efectos sobre las variables endógenas Y, P y r de una disminución del gasto fiscal. (\( Δ G_0 < 0 \)) . El análisis debe ser intuitivo, matemático y gráfico. En una figura, se debe que usar los ejes r e Y (modelo IS-LM), y en la otra, los ejes P y r (modelo DA-OA).

• Intuitivamente:

\[ G_0 ↓ → DA↓ → Y > DA → Y↓ \]

\[ Y↓ → M^d↓ → M^s > M^d → r↓ \]

Modelo DA-OA: $\( Y↓ → θ(Y-\bar{Y})↓ → P↓\)$

Con la reducción del gasto fiscal, la demanda agregada también se reduce. Asimismo, Y baja y la demanda de dinero disminuye.

• Matemáticamente:

# variables en simbolos IS
Co, Io, Go, Xo, h, r, b, m, t, beta_0, beta_1  = symbols('Co Io Go Xo h r b m t beta_0, beta_1')

# variables en simbolos LM 
k, j, Ms, P, Y = symbols('k j Ms P Y')

# nvariables en simbolos de oferta agregada
Pe, _Y, Y, θ = symbols('Pe, _Y, Y, θ')

# Beta_0 y beta_1
beta_0 = (Co + Io + Go + Xo)
beta_1 = ( 1-(b-m)*(1-t) )

# Producto de equilibrio en el modelo DA-OA
Y_eq = ( (1)/(θ + ( (j*beta_1+h*k)/h) ) )*( ( (h*Ms+j*beta_0)/h ) - Pe + θ*_Y )

# Precio de equilibrio en el modelo DA-OA 
P_eq = Pe + θ*(Y_eq - _Y)

# Tasa de interés de equilibrio en el modelo DA-OA
r_eq = (j*beta_0)/(k*h + j*beta_1) + ( h / (k*h + j*beta_1) )*(Ms - P_eq)
#((h*Ms+j*beta_0)/h) - ((j*beta_1+h*r)/h)*((P-Pe-θ*_Y)/θ)

# Cambio del Gasto Fiscal sobre el Producto
df_Y_eq_Go = diff(Y_eq, Go)
print("Δ del Producto con respecto al Δ de la masa monetaria = ", df_Y_eq_Go)
print("\n")

# Cambio del Gasto Fiscal sobre tasa de interes
df_r_eq_Go = diff(r_eq, Go)
print("Δ de la tasa de interés con respecto al Δ de la masa monetaria = ", df_r_eq_Go)
print("\n")

# Efecto del cambio del Gasto Fiscal sobre los Precios
df_P_eq_Go = diff(P_eq, Go)
print("Δ del nivel de precios con respecto al Δ de la masa monetaria = ", df_P_eq_Go)

Δ del Producto con respecto al Δ de la masa monetaria =  j/(h*(θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h))


Δ de la tasa de interés con respecto al Δ de la masa monetaria =  -j*θ/((θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h)*(h*k + j*(-(1 - t)*(b - m) + 1))) + j/(h*k + j*(-(1 - t)*(b - m) + 1))


Δ del nivel de precios con respecto al Δ de la masa monetaria =  j*θ/(h*(θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h))

Los Δ de Y, P y r son positivos. $\( ∆Y^eq = (+)(-) \)\( \)\( ∆r^eq = (+)(-) \)\( \)\( ∆P^eq = (+)(-) \)$

• Gráficamente:

# IS-LM

#1--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

Go = 20
r1 = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

#2--------------------------------------------------
# Curva LM ORIGINAL
# Parámetros

Y_size = 100
k = 2
j = 1                
Ms = 200             
P  = 8           

Y = np.arange(Y_size)

# Ecuación

def i_LM( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i = i_LM( k, j, Ms, P, Y)


#1--------------------------
# DA ORGINAL 
# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8
Ms = 200    

k = 2
j = 1                
Ms = 200             
P  = 8  

Y = np.arange(Y_size)


# Ecuación

B0 = Co + Io + Go + Xo
B1 = 1 - (b-m)*(1-t)

def P_AD(h, Ms, j, B0, B1, k, Y):
    P_AD = ((h*Ms + j*B0)/h) - (Y*(j*B1 + h*k)/h)
    return P_AD

P_AD = P_AD(h, Ms, j, B0, B1, k, Y)


#--------------------------------------------------
    # NUEVA Demanda Agregada

# Definir SOLO el parámetro cambiado

Go = 30
Ms = 200    
B0 = Co + Io + Go + Xo

# Generar la ecuación con el nuevo parámetro

def P_AD_Ms(h, Ms, j, B0, B1, k, Y):
    P_AD = ((h*Ms + j*B0)/h) - (Y*(j*B1 + h*k)/h)
    return P_AD

P_AD_G = P_AD_Ms(h, Ms, j, B0, B1, k, Y)

#2--------------------------
 # OA ORIGINAL
    
# Parámetros

Y_size = 100

Pe = 70
θ = 3
_Y = 20  

Y = np.arange(Y_size)

# Ecuación

def P_AS(Pe, _Y, Y, θ):
    P_AS = Pe + θ*(Y-_Y)
    return P_AS

P_AS = P_AS(Pe, _Y, Y, θ)

# Dos gráficos en un solo cuadro
fig, (ax1, ax2) = plt.subplots(2, figsize=(8, 16)) 

#---------------------------------
    # Gráfico 1: IS-LM
    
ax1.plot(Y, r, label = "IS", color = "C1") #IS
ax1.plot(Y, r1, label = "IS_G0", color = "C1", linestyle ='dashed') #IS
ax1.plot(Y, i, label="LM", color = "C0")  #LM


ax1.axvline(x=45,  ymin= 0, ymax= 1, linestyle = ":", color = "grey")
ax1.axvline(x=56,  ymin= 0, ymax= 1, linestyle = ":", color = "grey")
ax1.axhline(y=64,  xmin= 0, xmax= 0.44, linestyle = ":", color = "grey")
ax1.axhline(y=87,  xmin= 0, xmax= 0.56, linestyle = ":", color = "grey")

ax1.text(32, 100, '∆$Go$', fontsize=12, color='black')
ax1.text(26, 100, '←', fontsize=15, color='grey')

ax1.set(title="Efectos de una disminución en el gasto fiscal", xlabel= r'Y', ylabel= r'r')
ax1.legend()


#---------------------------------
    # Gráfico 2: DA-OA

ax2.plot(Y, P_AD, label = "AD", color = "C4") #DA
ax2.plot(Y, P_AD_G, label = "AD_G0", color = "C4", linestyle = 'dashed') #DA_Ms
ax2.plot(Y, P_AS, label = "AS", color = "C8") #OA

ax2.axvline(x=55,  ymin= 0, ymax= 1, linestyle = ":", color = "grey")
ax2.axvline(x=52,  ymin= 0, ymax= 1, linestyle = ":", color = "grey")
ax2.axhline(y=164,  xmin= 0, xmax= 0.51, linestyle = ":", color = "grey")
ax2.axhline(y=175,  xmin= 0, xmax= 0.56, linestyle = ":", color = "grey")

ax2.text(40, 160, '←', fontsize=15, color='grey')
ax2.text(35, 180, '∆$Go$', fontsize=12, color='black')


ax2.set(xlabel= r'Y', ylabel= r'P')
ax2.legend()

plt.show

<function matplotlib.pyplot.show(close=None, block=None)>

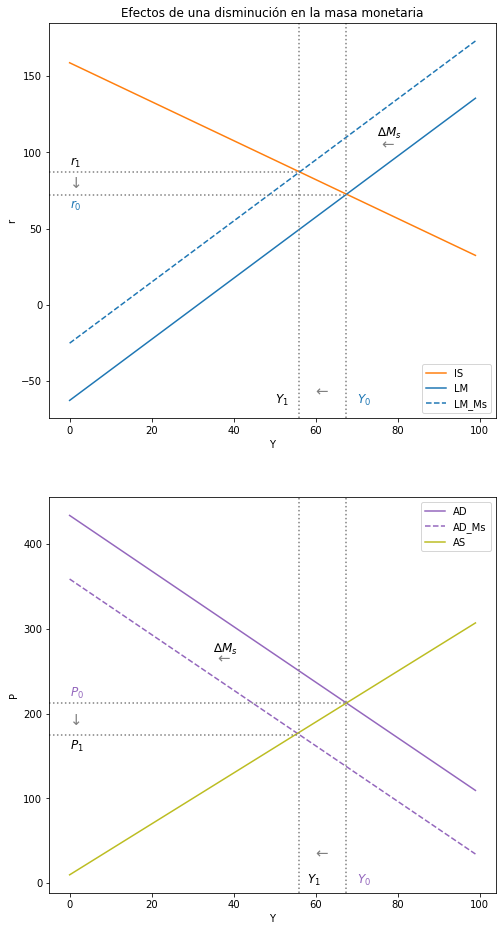
2. Analice los efectos sobre las variables endógenas Y, P yr de una disminución de la masa monetaria.(\( ΔM^s < 0 \)) . El análisis debe ser intuitivo, matemático y gráfico. En una figura, se debe que usar los ejes re Y (modelo IS-LM), y en la otra, los ejes P, Y (modelo DA-OA).

• Intuición:

Modelo IS-LM: $\( Ms↓ → M^s↓ → M^d > M^s → r↑ \)\( \)\( r↑ → I↓ → DA↓ → Y > DA → Y↓ \)$

Modelo DA-OA: $\( Y↓ → θ(Y-\bar{Y})↓ → P↓\)$

Con la disminución de la masa monetaria, se da exceso de demanda. Las inversiones caen y, por lo tanto, también lo hace la DA

• Matemáticamente:

# Variables en simbolos de IS
Co, Io, Go, Xo, h, r, b, m, t, beta_0, beta_1  = symbols('Co Io Go Xo h r b m t beta_0, beta_1')

# Variables en simbolos de LM 
k, j, Ms, P, Y = symbols('k j Ms P Y')

# aVriables en simbolos de oferta agregada
Pe, _Y, Y, θ = symbols('Pe, _Y, Y, θ')

# Beta_0 y beta_1
beta_0 = (Co + Io + Go + Xo)
beta_1 = ( 1-(b-m)*(1-t) )

# Producto de equilibrio en el modelo DA-OA
Y_eq = ( (1)/(θ + ( (j*beta_1+h*k)/h) ) )*( ( (h*Ms+j*beta_0)/h ) - Pe + θ*_Y )

# Precio de equilibrio en el modelo DA-OA 
P_eq = Pe + θ*(Y_eq - _Y)

# Tasa de interés de equilibrio en el modelo DA-OA
r_eq = (j*beta_0)/(k*h + j*beta_1) + ( h / (k*h + j*beta_1) )*(Ms - P_eq)
#((h*Ms+j*beta_0)/h) - ((j*beta_1+h*r)/h)*((P-Pe-θ*_Y)/θ)

# Cambio del Precio esperado sobre el Producto 
df_Y_eq_Ms = diff(Y_eq, Ms)
print("Δ del Producto con respecto al Δ de la masa monetaria = ", df_Y_eq_Ms)
print("\n")

# Cambio del Precio esperado sobre Tasa de Interés
df_r_eq_Ms = diff(r_eq, Ms)
print("Δ de la tasa de interés con respecto al Δ de la masa monetaria = ", df_r_eq_Ms)
print("\n")

# Cambio del Precio esperado sobre los Precios
df_P_eq_Ms = diff(P_eq, Ms)
print("Δ del nivel de precios con respecto al Δ de la masa monetaria = ", df_P_eq_Ms)

Δ del Producto con respecto al Δ de la masa monetaria =  1/(θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h)


Δ de la tasa de interés con respecto al Δ de la masa monetaria =  h*(-θ/(θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h) + 1)/(h*k + j*(-(1 - t)*(b - m) + 1))


Δ del nivel de precios con respecto al Δ de la masa monetaria =  θ/(θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h)

Los Δ de Y, P son positivos.

\[ ∆Y^eq = (+)(-) \]

\[ ∆r^eq = (-)(-) \]

\[ ∆P^eq = (+)(-) \]

• Gráficamente

# IS-LM

#1--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#2--------------------------------------------------
    # Curva LM ORIGINAL

# Parámetros

Y_size = 100

k = 2
j = 1                
Ms = 500             
P  = 8           

Y = np.arange(Y_size)

# Ecuación

def i_LM( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i = i_LM( k, j, Ms, P, Y)

#--------------------------------------------------
    # NUEVA curva LM: disminución en la Masa Monetaria (Ms)

# Definir SOLO el parámetro cambiado
Ms = 200

# Generar la ecuación con el nuevo parámetro
def i_LM_Ms( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i_Ms = i_LM_Ms( k, j, Ms, P, Y)

#DA-OA

#1--------------------------
    # Demanda Agregada ORGINAL
    
# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

k = 2
j = 1                
Ms = 275            
P  = 8  

Y = np.arange(Y_size)


# Ecuación

B0 = Co + Io + Go + Xo
B1 = 1 - (b-m)*(1-t)

def P_AD(h, Ms, j, B0, B1, k, Y):
    P_AD = ((h*Ms + j*B0)/h) - (Y*(j*B1 + h*k)/h)
    return P_AD

P_AD = P_AD(h, Ms, j, B0, B1, k, Y)

#--------------------------------------------------
    # NUEVA Demanda Agregada

# Definir SOLO el parámetro cambiado

Ms = 200

# Generar la ecuación con el nuevo parámetro

def P_AD_Ms(h, Ms, j, B0, B1, k, Y):
    P_AD = ((h*Ms + j*B0)/h) - (Y*(j*B1 + h*k)/h)
    return P_AD

P_Ms = P_AD_Ms(h, Ms, j, B0, B1, k, Y)


#2--------------------------
    # Oferta Agregada ORIGINAL
    
# Parámetros

Y_size = 100

Pe = 70
θ = 3
_Y = 20  

Y = np.arange(Y_size)

# Ecuación

def P_AS(Pe, _Y, Y, θ):
    P_AS = Pe + θ*(Y-_Y)
    return P_AS

P_AS = P_AS(Pe, _Y, Y, θ)

# Dos gráficos en un solo cuadro
fig, (ax1, ax2) = plt.subplots(2, figsize=(8, 16)) 

#---------------------------------
    # Gráfico 1: IS-LM
    
ax1.plot(Y, r, label = "IS", color = "C1") #IS
ax1.plot(Y, i, label="LM", color = "C0")  #LM
ax1.plot(Y, i_Ms, label="LM_Ms", color = "C0", linestyle ='dashed')  #LM

ax1.axvline(x=67.5,  ymin= 0, ymax= 1, linestyle = ":", color = "grey")
ax1.axvline(x=56,  ymin= 0, ymax= 1, linestyle = ":", color = "grey")
ax1.axhline(y=72,  xmin= 0, xmax= 0.66, linestyle = ":", color = "grey")
ax1.axhline(y=87,  xmin= 0, xmax= 0.56, linestyle = ":", color = "grey")

ax1.text(75, 110, '∆$M_s$', fontsize=12, color='black')
ax1.text(76, 102, '←', fontsize=15, color='grey')
ax1.text(60, -60, '←', fontsize=15, color='grey')
ax1.text(0, 77, '↓', fontsize=15, color='grey')
ax1.text(50, -65, '$Y_1$', fontsize=12, color='black')
ax1.text(70, -65, '$Y_0$', fontsize=12, color='C0')
ax1.text(0, 91, '$r_1$', fontsize=12, color='black')
ax1.text(0, 63, '$r_0$', fontsize=12, color='C0')


ax1.set(title="Efectos de una disminución en la masa monetaria", xlabel= r'Y', ylabel= r'r')
ax1.legend()


#---------------------------------
    # Gráfico 2: DA-OA

ax2.plot(Y, P_AD, label = "AD", color = "C4") #DA
ax2.plot(Y, P_Ms, label = "AD_Ms", color = "C4", linestyle = 'dashed') #DA_Ms
ax2.plot(Y, P_AS, label = "AS", color = "C8") #OA

ax2.axvline(x=67.5,  ymin= 0, ymax= 1, linestyle = ":", color = "grey")
ax2.axvline(x=56,  ymin= 0, ymax= 1, linestyle = ":", color = "grey")
ax2.axhline(y=213,  xmin= 0, xmax= 0.67, linestyle = ":", color = "grey")
ax2.axhline(y=175,  xmin= 0, xmax= 0.56, linestyle = ":", color = "grey")

ax2.text(60, 30, '←', fontsize=15, color='grey')
ax2.text(36, 260, '←', fontsize=15, color='grey')
ax2.text(35, 272, '∆$M_s$', fontsize=12, color='black')
ax2.text(0, 187, '↓', fontsize=15, color='grey')

ax2.text(58, 0, '$Y_1$', fontsize=12, color='black')
ax2.text(70, 0, '$Y_0$', fontsize=12, color='C4')
ax2.text(0, 158, '$P_1$', fontsize=12, color='black')
ax2.text(0, 220, '$P_0$', fontsize=12, color='C4')

ax2.set(xlabel= r'Y', ylabel= r'P')
ax2.legend()

plt.show

<function matplotlib.pyplot.show(close=None, block=None)>

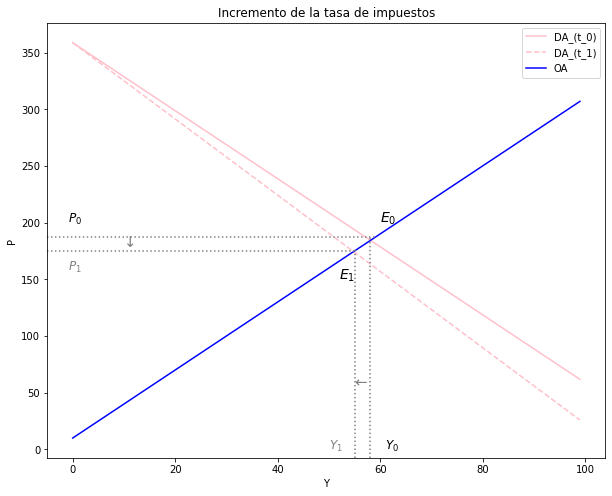
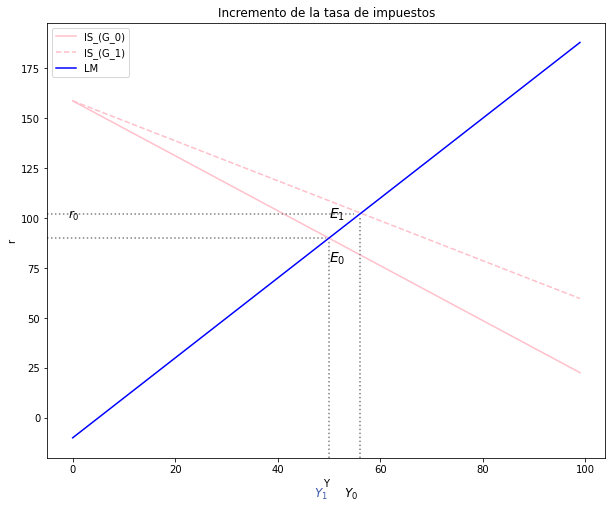
3. Analice los efectos sobre las variables endógenas Y, P y r de un incremento de la tasa de impuestos(\( Δt > 0 \)) El análisis debe ser intuitivo, matemático y gráfico. En una figura, se debe que usar los ejes r e Y (modelo IS-LM), y en la otra, los ejes P, Y (modelo DA-OA).

• Intuición:

Modelo IS-LM: $\( t↑ → DA↓ → Y > DA → Y↓ \)\( \)\( Y↓ → M^d↓ → M^s > M^d → r↓ \)$

Modelo DA-OA: $\( Y↓ → θ(Y-\bar{Y})↓ → P↓\)$

Con el aumento de la tasa de impuestos, la DA disminuye.

• Matemática:

# variables como símbolos IS
Co, Io, Go, Xo, h, r, b, m, t, beta_0, beta_1  = symbols('Co Io Go Xo h r b m t beta_0, beta_1')

# variables como símbolos LM 
k, j, Ms, P, Y = symbols('k j Ms P Y')

# variables como símbolos para oferta agregada
Pe, _Y, Y, θ = symbols('Pe, _Y, Y, θ')

# Beta_0 y beta_1
beta_0 = (Co + Io + Go + Xo)
beta_1 = ( 1-(b-m)*(1-t) )

# Producto de equilibrio en el modelo DA-OA
Y_eq = ( (1)/(θ + ( (j*beta_1+h*k)/h) ) )*( ( (h*Ms+j*beta_0)/h ) - Pe + θ*_Y )

# Precio de equilibrio en el modelo DA-OA 
P_eq = Pe + θ*(Y_eq - _Y)

# Tasa de interés de equilibrio en el modelo DA-OA
r_eq = (j*beta_0)/(k*h + j*beta_1) + ( h / (k*h + j*beta_1) )*(Ms - P_eq)
#((h*Ms+j*beta_0)/h) - ((j*beta_1+h*r)/h)*((P-Pe-θ*_Y)/θ)

# Cambio de Precio esperado sobre el Producto 
df_Y_eq_t = diff(Y_eq, t)
print("Δ del Producto con respecto al Δ de la masa monetaria = ", df_Y_eq_t)
print("\n")

# Cambio de Precio esperado sobre Tasa de Interés
df_r_eq_t = diff(r_eq, t)
print("Δ de la tasa de interés con respecto al Δ de la masa monetaria = ", df_r_eq_t)
print("\n")

# Cambio de Precio esperado sobre los Precios
df_P_eq_t = diff(P_eq, t)
print("Δ del nivel de precios con respecto al Δ de la masa monetaria = ", df_P_eq_t)

Δ del Producto con respecto al Δ de la masa monetaria =  -j*(b - m)*(-Pe + _Y*θ + (Ms*h + j*(Co + Go + Io + Xo))/h)/(h*(θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h)**2)


Δ de la tasa de interés con respecto al Δ de la masa monetaria =  -h*j*(b - m)*(Ms - Pe - θ*(-_Y + (-Pe + _Y*θ + (Ms*h + j*(Co + Go + Io + Xo))/h)/(θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h)))/(h*k + j*(-(1 - t)*(b - m) + 1))**2 - j**2*(b - m)*(Co + Go + Io + Xo)/(h*k + j*(-(1 - t)*(b - m) + 1))**2 + j*θ*(b - m)*(-Pe + _Y*θ + (Ms*h + j*(Co + Go + Io + Xo))/h)/((θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h)**2*(h*k + j*(-(1 - t)*(b - m) + 1)))


Δ del nivel de precios con respecto al Δ de la masa monetaria =  -j*θ*(b - m)*(-Pe + _Y*θ + (Ms*h + j*(Co + Go + Io + Xo))/h)/(h*(θ + (h*k + j*(-(1 - t)*(b - m) + 1))/h)**2)

Los Δ de Y, P y r son negativos.

\[ ∆Y^eq = (-)(+) \]

\[ ∆r^eq = (-)(+) \]

\[ ∆P^eq = (-)(+) \]

Gráficamente:

#IS-LM
# Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.001

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#2--------------------------------------------------
    # Curva LM ORIGINAL

# Parámetros

Y_size = 100

k = 2
j = 1                
Ms = 200             
P  = 20               

Y = np.arange(Y_size)

# Ecuación

def i_LM( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i = i_LM( k, j, Ms, P, Y)

#--------------------------------------------------
    # NUEVA curva IS: incremento de la tasa de impuestos (t)
    
# Definir SOLO el parámetro cambiado
t = 3

# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_G = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


# Gráfico

# Dimensiones del gráfico
y_max = np.max(i)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS_(G_0)", color = "pink") #IS_orginal
ax.plot(Y, r_G, label = "IS_(G_1)", color = "pink", linestyle = 'dashed') #IS_modificada

ax.plot(Y, i, label="LM", color = "blue")  #LM_original

# Texto y figuras agregadas
plt.axvline(x=50,  ymin= 0, ymax= 0.50, linestyle = ":", color = "grey")
plt.axhline(y=90, xmin= 0, xmax= 0.50, linestyle = ":", color = "grey")

plt.axvline(x=56,  ymin= 0, ymax= 0.55, linestyle = ":", color = "grey")
plt.axhline(y=102, xmin= 0, xmax= 0.55, linestyle = ":", color = "grey")
plt.text(50,100, '$E_1$', fontsize = 14, color = 'black')

plt.text(50,78, '$E_0$', fontsize = 14, color = 'black')
plt.text(-1,100, '$r_0$', fontsize = 12, color = 'black')
plt.text(53,-40, '$Y_0$', fontsize = 12, color = 'black')
plt.text(47,-40, '$Y_1$', fontsize = 12, color = '#3D59AB')

#plt.text(69, 115, '→', fontsize=15, color='grey')
#plt.text(69, 52, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title="Incremento de la tasa de impuestos", xlabel= r'Y', ylabel= r'r')
ax.legend()

plt.show()

#DA-OA

#1--------------------------
    # Demanda Agregada ORGINAL
    
# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.1

k = 2
j = 1                
Ms = 200             
P  = 8  

Y = np.arange(Y_size)


# Ecuación

B0 = Co + Io + Go + Xo
B1 = 1 - (b-m)*(1-t)

def P_AD(h, Ms, j, B0, B1, k, Y):
    P_AD = ((h*Ms + j*B0)/h) - (Y*(j*B1 + h*k)/h)
    return P_AD

P_AD_t = P_AD(h, Ms, j, B0, B1, k, Y)


#2--------------------------
    # Oferta Agregada ORIGINAL
    
# Parámetros

Y_size = 100

Pe = 70
θ = 3
_Y = 20  

Y = np.arange(Y_size)

# Ecuación

def P_AS(Pe, _Y, Y, θ):
    P_AS = Pe + θ*(Y-_Y)
    return P_AS

P_AS_t = P_AS(Pe, _Y, Y, θ)

#--------------------------------------------------
    # NUEVA Demanda Agregada

# Definir SOLO el parámetro cambiado

t = 3

B1 = 1 - (b-m)*(1-t)

# Generar la ecuación con el nuevo parámetro

def P_AD(h, Ms, j, B0, B1, k, Y):
    P_AD = ((h*Ms + j*B0)/h) - (Y*(j*B1 + h*k)/h)
    return P_AD

P_AD_t1 = P_AD(h, Ms, j, B0, B1, k, Y)

# Gráfico

# Dimensiones del gráfico
y_max = np.max(P_AS_t)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, P_AD_t1, label = "DA_(t_0)", color = "pink") 
ax.plot(Y, P_AD_t, label = "DA_(t_1)", color = "pink", linestyle = 'dashed')

ax.plot(Y, P_AS_t, label="OA", color = "blue")  

# Texto y figuras agregadas
plt.axvline(x=55,  ymin= 0, ymax= 0.48, linestyle = ":", color = "grey")
plt.axhline(y=175, xmin= 0, xmax= 0.55, linestyle = ":", color = "grey")

plt.axvline(x=58,  ymin= 0, ymax= 0.51, linestyle = ":", color = "grey")
plt.axhline(y=187, xmin= 0, xmax= 0.59, linestyle = ":", color = "grey")

plt.text(52,150, '$E_1$', fontsize = 14, color = 'black')
plt.text(60,200, '$E_0$', fontsize = 14, color = 'black')
plt.text(-1,200, '$P_0$', fontsize = 12, color = 'black')
plt.text(-1,158, '$P_1$', fontsize = 12, color = 'grey')
plt.text(61,0, '$Y_0$', fontsize = 12, color = 'black')
plt.text(50, 0, '$Y_1$', fontsize = 12, color = 'grey')

plt.text(55, 55, '←', fontsize=15, color='grey')
plt.text(10, 179, '↓', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title="Incremento de la tasa de impuestos", xlabel= r'Y', ylabel= r'P')
ax.legend()

plt.show()