Capítulo 3: El Mercado Monetario y la Curva LM
Contents
Capítulo 3: El Mercado Monetario y la Curva LM#
PARTE 1: Lectura de Mendoza, W., Mancilla, L., & Velarde, R. (2021). La Macroeconomía de la cuarentena: Un modelo de dos sectores. Pontificia Universidad Católica del Perú.#
Mendoza, Mancilla y Velarde (2021) en su artículo “La Macroeconomía de la cuarentena: Un modelo de dos sectores”, parten por la cuestión de ¿cuáles fueron los efectos de la cuarentena en la economía peruana?. Para entrar en contexto, la problemática parte por la preocupante caída del PBI en 11% en el 2020 a causa de la COVID-19. Frente a este escenario de preocupación sanitaria global, el gobierno peruano sugiere un instrumento para contenerla: la cuarentena.
Para responder a esta pregunta, los autores proponen un modelo macroeconómico de dos sectores (inspirado en Blanchard, 2021) para reproducir los hechos mencionados. Los dos sectores que presentan se tratan de sectores keynesianos; es decir, la producción es determinada por la demanda y los niveles de los precios son dependientes del nivel que se espera de estos y de la brecha del PBI por sector.
Los autores distinguen dos sectores para propósitos de este análisis, el sector 1, es el ámbito afectado de manera directa por el cese de actividades durante las medidas de aislamiento. El sector 2, es aquel que pudo seguir laborando durante la cuarentena, pero se ve afectado por la demanda del sector 1. Asimismo, se señala que este modelo puede ser útil para simular los efectos del fin de la cuarentena. La distinción propuesta entre estos dos sectores me parece muy apropiada y, además, corresponde a un punto fuerte para responder a la pregunta de investigación.
Seguidamente, los autores presentan subsistemas del modelo elaborado: el corto plazo, el equilibrio estacionario y el tránsito hacia el equilibrio estacionario. En este ejercicio se observa que, para el sector 1, la caída del producto potencial y el consumo autónomo son permanentes, lo que supone que sus nuevos niveles se encuentran en equilibrio estacionario. Se entiende que, después de la caída en la producción y en los precios (en los dos sectores), la economía logra recuperarse. Esta recuperación se da continuamente hasta alcanzar un nuevo equilibrio estacionario.
Posteriormente, los autores realizan un segundo ejercicio donde se simulan los efectos de la cuarentena, suponiendo una caída del PBI potencial en el sector 1 (y por lo tanto, una caída del consumo autónomo); asimismo, se exploran los efectos para revertir estos hechos. En este segundo ejercicio, notamos que las caídas mencionadas no son permanentes sino transitorias; esperando así que los precios vuelvan a su nivel inicial. Este escenario alentador, se debe a que según los autores, nuestro país implementó una política crediticia muy potente entre 2020 y 2021; evitando así la quiebra de muchas empresas. Considerar la política crediticia peruana para la recuperación del PBI, me pareció un punto positivo del artículo; sin embargo, un aspecto negativo es que no se logró explorar a profundidad.
El avance de Mendoza, Mancilla y Velarde, para responder a la cuestión que plantean al inicio, es muy fructífero y aborda muchos puntos importantes que contribuyen al análisis macroeconómico del impacto de la cuarentena en el país. Sin embargo, propongo algunos pasos más para el análisis en base a la lectura de otros autores. En primer lugar, sugeriría un análisis a profundidad del impacto de la política fiscal como respuesta del país a la cuarentena a corto plazo; es decir, no solo incorporar el factor de la política crediticia a favor de las empresas, sino también la política de bonos extraordinarios a la población. Esta propuesta parte de mi análisis del informe de CEPAL del país al 2021 sobre el Estudio Económico de América Latina y el Caribe. Finalmente, siguiendo la propuesta de modelo macroeconómico de Asiain (2020) sobre el caso de la “Macroeconomía en cuarentena en Argentina”, sugiero que sería importante añadir al modelo de Mendoza, Mancilla y Velarde la sostenibilidad a largo plazo del modelo macroeconómico; pues estos autores sólo habían considerado el factor a corto plazo.
PARTE 2: Código en Python -#
Código hecho por Karen Arevalo y Mayeli Charra#
Explique las características de los instrumentos de política monetaria que pueden utilizar el Banco Central.#
En principio, el Banco Central al ser la autoridad monetaria del sistema bancario, tiene la capacidad suficiente para el control y el gestionamiento de la oferta monetaria. En ese sentido, realiza políticas monetarias expansivas o contractivas a través de tres posibles instrumentos:
La Oferta Monetaria (como instrumento de política):
Con el propósito de aumentar o disminuir la oferta, se emplea la Operación de Mercado Abierto. El Banco Central se encarga de realizar estas operaciones por medio de la compra o la venta de activos financieros o bonos a los bancos comerciales. Aquí podemos distinguir:
- Política Monetaria Expansiva:
La cual se da mediante la compra de bonos del mercado, inyectando así a la economía. Dentro del balance del Banco Central, se notará un incremento de sus activos, lo que genera un incremento de los depósitos de los bancos comerciales en el BC. Por lo tanto, esta operación se cracteriza por aumentar la base monetaria y la oferta monetaris.
- Política Monetaria Contractiva:
Se da mediante la venta de bonos al mercado. A través de esto proceso, el Banco Central retira dinero de la economía. Dentro del balance del Banco Central, se notará una disminución de los depósitos de los bancos comerciales; por lo que, se reduce la base y la oferta monetarias.
El coeficiente legal de encaje (como instrumento de política):
A parte de las operaciones de mercado abierto, el BC también dispone como instrumento al coeficiente legal de encaje. Mostrandose así:
- Política Monetaria Expansiva:
El BC genera un aumento de la cantidad de dinero que disponen los bancos para efectuar préstamos a través de la disminución de la tasa de encaje. Pues, porque esto implica que el resto de bancos comerciales tengan menos dinero en forma de reserva dentro del balance del BC. En consecuencia, la disminución de la tasa de encaje aumenta la posibilidad de generar dinero bancario (ya que aumenta el multiplicador, y este aumenta la oferta de dinero).
- Política Monetaria Contractiva:
Se produce cuando el Banco Central aumenta el coeficiente de encaje; ello implica que, los bancos comerciales tengan mayor proporción de dinero en forma de reserva en el balance del BC. En ese sentido, se reduce el multiplicador bancario y disminuye la oferta monetaria.
La tasa de interés (como instrumento de política):
A través de este instrumento, los Bancos Centrales apuestan por un nuevo esquema de política monetaria, pasando a la oferta monetaria como una variable endógena. La tasa de política, es la tasa de interés de referencia de la política monetaria.
- Política Monetaria Expansiva:
El BC se encarga de hacer una política monetaria expansiva que reduce su tasa de interés de referencia. Así, aumenta la cantidad de dinero en soles prestada a los otros bancos comerciales y se aumenta la base y la oferta monetarias.
- Política Monetaria Contractiva:
El BC se encarga de hacer una política monetaria contractiva que aumenta la tasa de interés de referencia. Así, disminuye la cantidad de dinero en préstamo (al crédito), reduciendo la base y la oferta monetarias.
Derive la oferta real de dinero y explique cada uno de sus componentes.#
La oferta nominal de dinero, denominada (\(M^s\)) es una variable exógena e instrumento de politica monetaria.
Entre sus componentes esta: \(M_0^s\): la cuál representa la oferta monetaria constituida por el total de dinero líquido en circulación y el dinero bancario.
Para que esta sea expresada en terminos reales se debe dividir entre el nivel general de precios de la economía representa por \(p\)
De esta forma se obtiene que la oferta real de dinero se representa así:
Derive la demanda real de dinero. Explique qué papel cumplen los parámetros “k” y “j”#
La función de la demanda real está dada por:
En la función de la demanda real, “k” indica la magnitud del parámetro, es decir, la sensibilidad de la demanda de dinero. “j” indica cuán sensibles es la demanda de dinero ante las variaciones de la tasa de interés.
Asumiendo que no hay inflación podemos asumir que \( i = r \). Escriba en terminos reales la eucacion de equilibrio en el mercado de dinero.#
Sabiendo que \(i = r\)
Ecuación de equilibrio:
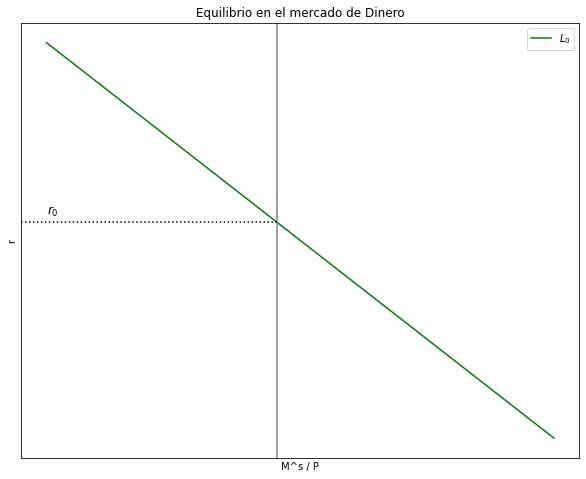
Grafique el equilibrio en el mercado de dinero.#
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import sympy as sy
import pandas as pd
import numpy as np
import random
import math
import sklearn
import scipy as sp
import networkx
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.iolib.summary2 import summary_col
from causalgraphicalmodels import CausalGraphicalModel
---------------------------------------------------------------------------
KeyboardInterrupt Traceback (most recent call last)
Input In [1], in <cell line: 11>()
9 import sklearn
10 import scipy as sp
---> 11 import networkx
12 import statsmodels.api as sm
13 import statsmodels.formula.api as smf
File ~\anaconda3\lib\site-packages\networkx\__init__.py:55, in <module>
51 raise AttributeError(f"module {__name__} has no attribute {name}")
54 # These are imported in order as listed
---> 55 from networkx.lazy_imports import lazy_import
57 from networkx.exception import *
59 from networkx import utils
File <frozen importlib._bootstrap>:1007, in _find_and_load(name, import_)
File <frozen importlib._bootstrap>:986, in _find_and_load_unlocked(name, import_)
File <frozen importlib._bootstrap>:680, in _load_unlocked(spec)
File <frozen importlib._bootstrap_external>:846, in exec_module(self, module)
File <frozen importlib._bootstrap_external>:941, in get_code(self, fullname)
File <frozen importlib._bootstrap_external>:1040, in get_data(self, path)
KeyboardInterrupt:
# Parámetross
r_size = 100
k = 0.5
j = 0.2
P = 10
Y = 35
r = np.arange(r_size)
# Ecuación
def Ms_MD(k, j, P, r, Y):
Ms_MD = P*(k*Y - j*r)
return Ms_MD
Ms_MD = Ms_MD(k, j, P, r, Y)
# Equilibrio en el mercado de dinero
fig, ax1 = plt.subplots(figsize=(10, 8))
ax1.set(title="Equilibrio en el mercado de Dinero", xlabel=r'M^s / P', ylabel=r'r')
ax1.plot(Ms_MD, label= '$L_0$', color = 'green')
ax1.axvline(x = 45, ymin= 0, ymax= 1, color = "grey")
ax1.axhline(y=85, xmin= 0, xmax= 0.46, linestyle = ":", color = "black")
ax1.text(0, 89, "$r_0$", fontsize = 12, color = 'black')
ax1.yaxis.set_major_locator(plt.NullLocator())
ax1.xaxis.set_major_locator(plt.NullLocator())
ax1.legend()
plt.show()
Efectos dentro dentro del Mercado de Dinero (Enfocarse en la demanda y oferta de dinero, siguiendo el grafico en 5)#
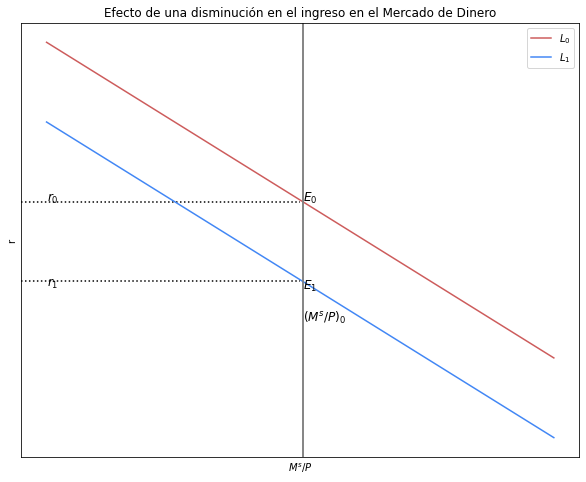
Explique y grafique qué sucede en el mercado de dinero si \( ΔY < 0 \)#
Explicación: Cuando disminuye el ingreso “Y”, la demanda de dinero también disminuye. Si el mercado se encontraba en equilibrio, esta disminución genera disminución de demanda en el mercado. La curva de la demanda de dinero se desplazará hacia abajo.
# Parametros con cambio en el Y
r_size = 100
k = 0.5
j = 0.2
P = 10
Y_1 = 25
MS_0 = 500
r = np.arange(r_size)
# Necesitamos crear la funcion de demanda
def MD(k, j, P, r, Y):
MD_eq = (k*Y - j*r)
return MD_eq
MD_1 = MD(k, j, P, r, Y_1)
# Necesitamos crear la oferta de dinero.
MS = MS_0 / P
MS
# Equilibrio en el mercado de dinero
# Creamos el seteo para la figura
fig, ax1 = plt.subplots(figsize=(10, 8))
# Agregamos titulo t el nombre de las coordenadas
ax1.set(title="Efecto de una disminución en el ingreso en el Mercado de Dinero", xlabel=r'$M^s / P$', ylabel=r'r')
# Ploteamos la demanda de dinero
ax1.plot(MD_0, label= '$L_0$', color = '#CD5C5C')
#ax1.plot(MD_1, label= '$L_0$', color = '#CD5C5C')
# Para plotear la oferta de dinero solo necesitamos crear una linea vertical
ax1.axvline(x = MS, ymin= 0, ymax= 1, color = "grey")
# Creamos las lineas puntadas para el equilibrio
ax1.axhline(y=7.5, xmin= 0, xmax= 0.5, linestyle = ":", color = "black")
# Agregamos texto
ax1.text(0, 7.5, "$r_0$", fontsize = 12, color = 'black')
ax1.text(50, 0, "$(M^s/P)_0$", fontsize = 12, color = 'black')
ax1.text(50, 7.5, "$E_0$", fontsize = 12, color = 'black')
# Nuevas curvas a partir del cambio en el nivel del producto
ax1.plot(MD_1, label= '$L_1$', color = '#4287f5')
ax1.axvline(x = MS, ymin= 0, ymax= 1, color = "grey")
ax1.axhline(y=2.5, xmin= 0, xmax= 0.5, linestyle = ":", color = "black")
ax1.text(0, 2.2, "$r_1$", fontsize = 12, color = 'black')
ax1.text(50, 2, "$E_1$", fontsize = 12, color = 'black')
ax1.yaxis.set_major_locator(plt.NullLocator())
ax1.xaxis.set_major_locator(plt.NullLocator())
ax1.legend()
plt.show()
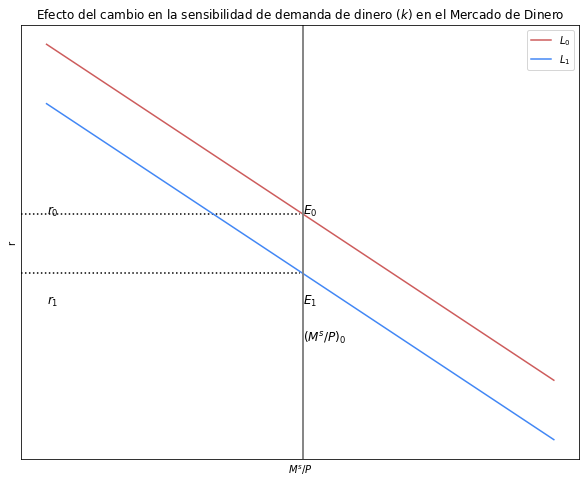
Explique y grafique qué sucede en el mercado de dinero si \(Δk<0\)#
# Parameters con cambio en k
r_size = 100
k_1 = 0.4
j = 0.2
P = 10
Y = 35
MS_0 = 500
r = np.arange(r_size)
# Necesitamos crear la funcion de demanda
def MD(k_1, j, P, r, Y):
MD_eq = (k_1*Y - j*r)
return MD_eq
MD_1 = MD(k_1, j, P, r, Y)
# Necesitamos crear la oferta de dinero.
MS = MS_0 / P
MS
# Equilibrio en el mercado de dinero
# Creamos el seteo para la figura
fig, ax1 = plt.subplots(figsize=(10, 8))
# Agregamos titulo t el nombre de las coordenadas
ax1.set(title="Efecto del cambio en la sensibilidad de demanda de dinero $(k)$ en el Mercado de Dinero", xlabel=r'$M^s / P$', ylabel=r'r')
# Ploteamos la demanda de dinero
ax1.plot(MD_0, label= '$L_0$', color = '#CD5C5C')
#ax1.plot(MD_1, label= '$L_0$', color = '#CD5C5C')
# Para plotear la oferta de dinero solo necesitamos crear una linea vertical
ax1.axvline(x = MS, ymin= 0, ymax= 1, color = "grey")
# Creamos las lineas puntadas para el equilibrio
ax1.axhline(y=7.5, xmin= 0, xmax= 0.5, linestyle = ":", color = "black")
# Agregamos texto
ax1.text(0, 7.5, "$r_0$", fontsize = 12, color = 'black')
ax1.text(50, 0, "$(M^s/P)_0$", fontsize = 12, color = 'black')
ax1.text(50, 7.5, "$E_0$", fontsize = 12, color = 'black')
# Nuevas curvas a partir del cambio en el nivel del producto
ax1.plot(MD_1, label= '$L_1$', color = '#4287f5')
ax1.axvline(x = MS, ymin= 0, ymax= 1, color = "grey")
ax1.axhline(y=4, xmin= 0, xmax= 0.5, linestyle = ":", color = "black")
ax1.text(0, 2.2, "$r_1$", fontsize = 12, color = 'black')
ax1.text(50, 2.2, "$E_1$", fontsize = 12, color = 'black')
ax1.yaxis.set_major_locator(plt.NullLocator())
ax1.xaxis.set_major_locator(plt.NullLocator())
ax1.legend()
plt.show()
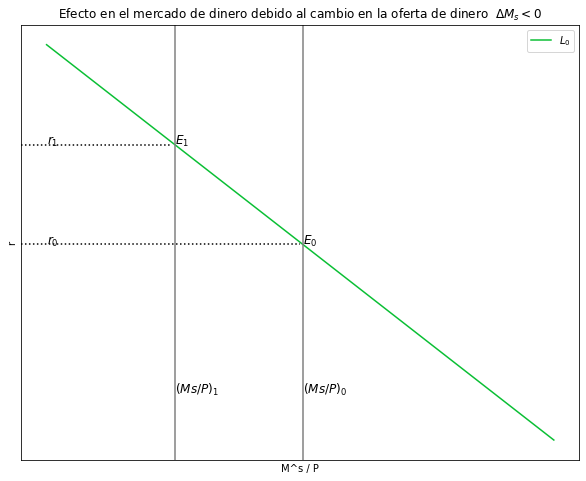
Explique y grafique qué sucede en el mercado de dinero si \(ΔM_s<0\)#
Si la oferta de dinero cambia el mercado de dinero (la recta vertical) se desplaza de manera horizontal.
# Parameters con cambio en el nivel del producto
r_size = 100
k = 0.5
j = 0.2
P_1 = 10
Y = 35
MS_1 = 80
r = np.arange(r_size)
# Necesitamos crear la funcion de demanda
def MD(k, j, P, r, Y):
MD_eq = (k*Y - j*r)
return MD_eq
MD_1 = MD(k, j, P_1, r, Y)
# Necesitamos crear la oferta de dinero.
MS_1 = MS_0 / P_1
MS
50.0
# Equilibrio en el mercado de dinero
# Creamos el seteo para la figura
fig, ax1 = plt.subplots(figsize=(10, 8))
# Agregamos titulo t el nombre de las coordenadas
ax1.set(title="Efecto en el mercado de dinero debido al cambio en la oferta de dinero $ΔM_s<0$", xlabel=r'M^s / P', ylabel=r'r')
# Ploteamos la demanda de dinero
ax1.plot(MD_0, label= '$L_0$', color = '#0abf34')
#ax1.plot(MD_1, label= '$L_0$', color = '#CD5C5C')
# Para plotear la oferta de dinero solo necesitamos crear una linea vertical
ax1.axvline(x = 50, ymin= 0, ymax= 1, color = "grey")
# Creamos las lineas puntadas para el equilibrio
ax1.axhline(y=7.5, xmin= 0, xmax= 0.5, linestyle = ":", color = "black")
# Agregamos texto
ax1.text(0, 7.5, "$r_0$", fontsize = 12, color = 'black')
ax1.text(50, 0, "$(Ms/P)_0$", fontsize = 12, color = 'black')
ax1.text(50, 7.5, "$E_0$", fontsize = 12, color = 'black')
# Nuevas curvas a partir del cambio en la oferta
#ax1.plot(MD_1, label= '$L_1$', color = '#4287f5')
ax1.axvline(x = 25, ymin= 0, ymax= 1, color = "grey")
ax1.axhline(y=12.5, xmin= 0, xmax= 0.27 , linestyle = ":", color = "black")
ax1.text(0, 12.5, "$r_1$", fontsize = 12, color = 'black')
ax1.text(25, 0, "$(Ms/P)_1$", fontsize = 12, color = 'black')
ax1.text(25, 12.5, "$E_1$", fontsize = 12, color = 'black')
ax1.yaxis.set_major_locator(plt.NullLocator())
ax1.xaxis.set_major_locator(plt.NullLocator())
ax1.legend()
plt.show()
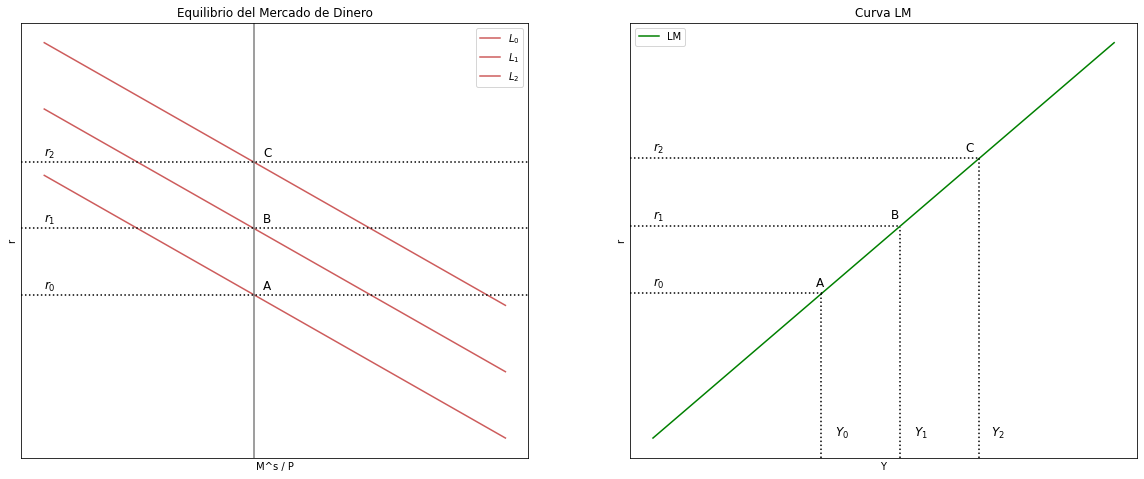
Curva LM#
Derive paso a paso la curva LM matemáticamente (a partir del equilibrio en el Mercado Monetario) y grafique.#
Sabiendo que la Curva LM dicta todos los puntos de equilibrio en el mercado monetario y que:
Ecuación 1:
Ecuación 2:
Punto de equilibrio: \( M^d = M^s \)
#1----------------------Equilibrio mercado monetario
# Parameters
r_size = 100
k = 0.5
j = 0.2
P = 10
Y = 35
r = np.arange(r_size)
# Ecuación
def Ms_MD(k, j, P, r, Y):
Ms_MD = P*(k*Y - j*r)
return Ms_MD
Ms_MD = Ms_MD(k, j, P, r, Y)
# Nuevos valores de Y
Y1 = 45
def Ms_MD_Y1(k, j, P, r, Y1):
Ms_MD = P*(k*Y1 - j*r)
return Ms_MD
Ms_Y1 = Ms_MD_Y1(k, j, P, r, Y1)
Y2 = 25
def Ms_MD_Y2(k, j, P, r, Y2):
Ms_MD = P*(k*Y2 - j*r)
return Ms_MD
Ms_Y2 = Ms_MD_Y2(k, j, P, r, Y2)
#2----------------------Curva LM
# Parameters
Y_size = 100
k = 0.5
j = 0.2
P = 10
Ms = 30
Y = np.arange(Y_size)
# Ecuación
def i_LM( k, j, Ms, P, Y):
i_LM = (-Ms/P)/j + k/j*Y
return i_LM
i = i_LM( k, j, Ms, P, Y)
# Gráfico de la derivación de la curva LM a partir del equilibrio en el mercado monetario
# Dos gráficos en un solo cuadro
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(20, 8))
#---------------------------------
# Gráfico 1: Equilibrio en el mercado de dinero
ax1.set(title="Equilibrio del Mercado de Dinero", xlabel=r'M^s / P', ylabel=r'r')
ax1.plot(Y, Ms_MD, label= '$L_0$', color = '#CD5C5C')
ax1.plot(Y, Ms_Y1, label= '$L_1$', color = '#CD5C5C')
ax1.plot(Y, Ms_Y2, label= '$L_2$', color = '#CD5C5C')
ax1.axvline(x = 45, ymin= 0, ymax= 1, color = "grey")
ax1.axhline(y=35, xmin= 0, xmax= 1, linestyle = ":", color = "black")
ax1.axhline(y=135, xmin= 0, xmax= 1, linestyle = ":", color = "black")
ax1.axhline(y=85, xmin= 0, xmax= 1, linestyle = ":", color = "black")
ax1.text(47, 139, "C", fontsize = 12, color = 'black')
ax1.text(47, 89, "B", fontsize = 12, color = 'black')
ax1.text(47, 39, "A", fontsize = 12, color = 'black')
ax1.text(0, 139, "$r_2$", fontsize = 12, color = 'black')
ax1.text(0, 89, "$r_1$", fontsize = 12, color = 'black')
ax1.text(0, 39, "$r_0$", fontsize = 12, color = 'black')
ax1.yaxis.set_major_locator(plt.NullLocator())
ax1.xaxis.set_major_locator(plt.NullLocator())
ax1.legend()
#---------------------------------
# Gráfico 2: Curva LM
ax2.set(title="Curva LM", xlabel=r'Y', ylabel=r'r')
ax2.plot(Y, i, label="LM", color = 'green')
ax2.axhline(y=160, xmin= 0, xmax= 0.69, linestyle = ":", color = "black")
ax2.axhline(y=118, xmin= 0, xmax= 0.53, linestyle = ":", color = "black")
ax2.axhline(y=76, xmin= 0, xmax= 0.38, linestyle = ":", color = "black")
ax2.text(67, 164, "C", fontsize = 12, color = 'black')
ax2.text(51, 122, "B", fontsize = 12, color = 'black')
ax2.text(35, 80, "A", fontsize = 12, color = 'black')
ax2.text(0, 164, "$r_2$", fontsize = 12, color = 'black')
ax2.text(0, 122, "$r_1$", fontsize = 12, color = 'black')
ax2.text(0, 80, "$r_0$", fontsize = 12, color = 'black')
ax2.text(72.5, -14, "$Y_2$", fontsize = 12, color = 'black')
ax2.text(56, -14, "$Y_1$", fontsize = 12, color = 'black')
ax2.text(39, -14, "$Y_0$", fontsize = 12, color = 'black')
ax2.axvline(x=70, ymin= 0, ymax= 0.69, linestyle = ":", color = "black")
ax2.axvline(x=53, ymin= 0, ymax= 0.53, linestyle = ":", color = "black")
ax2.axvline(x=36, ymin= 0, ymax= 0.38, linestyle = ":", color = "black")
ax2.yaxis.set_major_locator(plt.NullLocator())
ax2.xaxis.set_major_locator(plt.NullLocator())
ax2.legend()
plt.show()
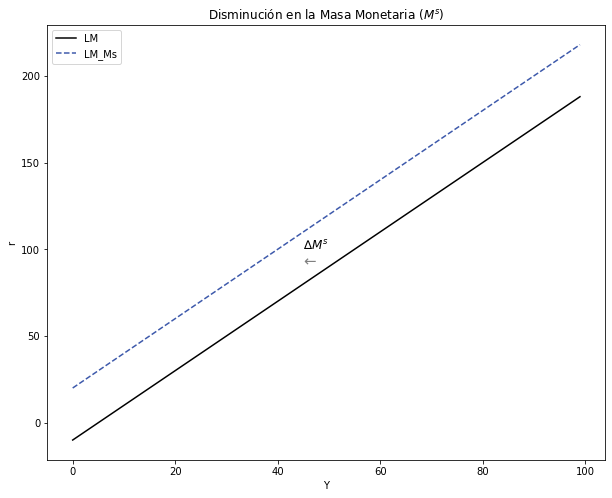
¿Cuál es el efecto de una disminución en la Masa Monetaria \( Δ M_s < 0 \) ? Explica usando la intuición y gráficos.#
Se trataría de una política monetaria contractiva.
Intuitivamente:
#--------------------------------------------------
# Curva LM ORIGINAL
# Parámetros
Y_size = 100
k = 2
j = 1
Ms = 200
P = 20
Y = np.arange(Y_size)
# Ecuación
def i_LM( k, j, Ms, P, Y):
i_LM = (-Ms/P)/j + k/j*Y
return i_LM
i = i_LM( k, j, Ms, P, Y)
#--------------------------------------------------
# NUEVA curva LM
# Definir SOLO el parámetro cambiado
Ms = -400
# Generar la ecuación con el nuevo parámetro
def i_LM_Ms( k, j, Ms, P, Y):
i_LM = (-Ms/P)/j + k/j*Y
return i_LM
i_Ms = i_LM_Ms( k, j, Ms, P, Y)
# Dimensiones del gráfico
y_max = np.max(i)
v = [0, Y_size, 0, y_max]
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, i, label="LM", color = 'black')
ax.plot(Y, i_Ms, label="LM_Ms", color = '#3D59AB', linestyle = 'dashed')
# Texto agregado
plt.text(45, 100, '∆$M^s$', fontsize=12, color='black')
plt.text(45, 90, '←', fontsize=15, color='grey')
# Título y leyenda
ax.set(title = "Disminución en la Masa Monetaria $(M^s)$", xlabel=r'Y', ylabel=r'r')
ax.legend()
plt.show()
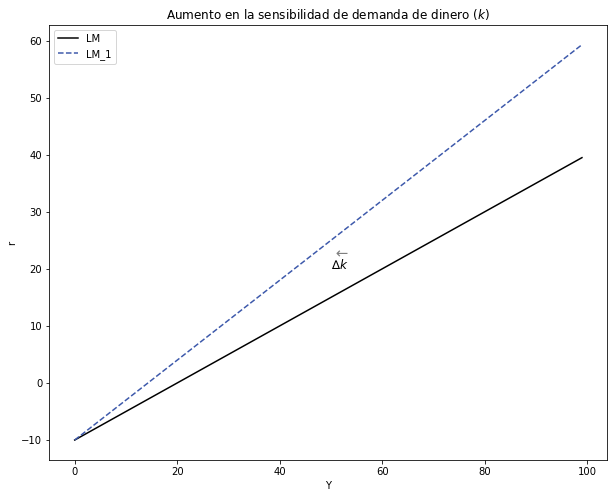
¿Cuál es el efecto de un aumento en \( Δk > 0 \) ? Explica usando intuición y gráficos.#
El efecto del aumento en la sensibilidad de la demanda de dinero, entonces la demanda de dinero aumenta, por lo tanto la pendiente de la curva aumenta.
- Intuición:#
- Gráfico:#
## Curva LM original
# Parámetros
Y_size = 100
k = 0.5
j = 1
Ms = 200
P = 20
Y = np.arange(Y_size)
# Ecuación
def i_LM( k, j, Ms, P, Y):
i_LM = (-Ms/P)/j + k/j*Y
return i_LM
i = i_LM( k, j, Ms, P, Y)
#--------------------------------------------------
# NUEVA curva LM
# Definir SOLO el parámetro cambiado
k = 0.7
# Generar la ecuación con el nuevo parámetro
def i_LM_Ms( k, j, Ms, P, Y):
i_LM = (-Ms/P)/j + k/j*Y
return i_LM
i_Ms = i_LM_Ms( k, j, Ms, P, Y)
# Dimensiones del gráfico
y_max = np.max(i)
v = [0, Y_size, 0, y_max]
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, i, label="LM", color = 'black')
ax.plot(Y, i_Ms, label="LM_1", color = '#3D59AB', linestyle = 'dashed')
# Texto agregado
plt.text(50, 20, '∆$k$', fontsize=12, color='black')
plt.text(50, 22, ' ←', fontsize=15, color='grey')
# Título y leyenda
ax.set(title = "Aumento en la sensibilidad de demanda de dinero $(k)$", xlabel=r'Y', ylabel=r'r')
ax.legend()
ax1.yaxis.set_major_locator(plt.NullLocator())
ax1.xaxis.set_major_locator(plt.NullLocator())
plt.show()