Capítulo 2: La Curva IS
Contents
Capítulo 2: La Curva IS#
PARTE 1: Lectura de Martinelli, C. y Vega, M. (2018). La Historia Monetaria y Fiscal del Perú, 1960-2017. Encuentro, (1/33).#
“The case of Peru” de Martinelli y Vega explora cómo el intervencionismo estatal influenció en la política monetaria para la expansión crediticia, la cual dio pase a múltiples medidas orientadas a expandir el desarrollo económico, pero que terminaron en la distorsión económica y en la aparición inflacionaria que provocó la caída de la productividad en el país.
Para responder y ahondar en esta cuestión, los autores proveen la interpretación de estos eventos teóricos por medio de los lentes del monetarismo. Desde esta perspectiva, la inflación, antes de la estabilización de 1990, refleja la necesidad fiscal de intereses inflacionarios en un régimen fiscal de dominación política monetaria.
Para demostrar todo lo anterior, realizan dos ejercicios de contabilidad. En primer lugar, a través del ejercicio de contabilidad de crecimiento, comprobaron que reformas como la intervención del estado y la interrupción de políticas fiscales en el periodo de los 70s-90s, condujeron a una mala asignación de recursos detrás de la caída masiva de la actividad de la productividad. Asimismo, sostienen que la depresión económica que sucumbió al país, puede ser explicada en términos de la caída de la productividad. En segundo lugar, Martinelli y Vega realizan un ejercicio de contabilidad fiscal. Dicho ejercicio demostró que los déficits fiscales se financiaron a través de la imposición inflacionista y de la acumulación de deuda externa, lo que con el tiempo produce una creciente necesidad de recurrir a la inflación. Sin embargo, fuera de estas nociones teóricas, creo que la historia es un poco más complicada que esto.
Además, los autores sugieren que los déficits fueron producto de una serie de gobiernos de carácter populista desde 1968. Los autores proponen que este periodo estuvo compuesto por dos fases. La fase 1 señalaría que los déficits de las empresas estatales fueron principalmente financiados por fondos externos, pero a su vez, fueron los cimientos para la financiación monetaria. La fase 2, apunta a que el gobierno de Alan García fue el responsable de llevar estas políticas al extremo y generar crisis de estanflación. Un aspecto que encuentro débil, es que en una parte de los capítulos de señoreaje (Capítulo 3), no se toma en cuenta el papel de los bancos públicos.
Por otro lado, es importante mencionar que el gobierno de Alan tuvo su oportunidad y su momento para intervenir ante la problemática que resaltan Martinelli y Vega, pero fracasó; consecuentemente, se desató la hiperinflación. Sería interesante poder ahondar porqué se dio esto, ¿existieron carencias monetarias distintas en esa época que influyeron en estas políticas erróneas?. Al respecto, la lectura de 1987 de Carbonetto, Dancourt (quien de paso fue una figura influyente durante el gobierno de Alan), y otros: “El Perú heterodoxo. Un modelo económico”, muestra un diagrama IS-LM donde la curva IS está inclinada hacia abajo. Es decir, es probable que ciertas creencias económicas en determinada época, hayan influido en la forma en la que se daban las políticas económicas. Según César Ferrari (2009), la economía heterodoxa (o poco convencional), tenía ciertos postulados poco tradicionales (como la curva de oferta con pendiente no positiva, el déficit fiscal no es inflacionario, las exportaciones no dependen del tipo de cambio, etc).
Finalmente, hubiera sido interesante que la lectura de Martinelli y Vega haya hecho hincapié también en estos aspectos. Sin embargo, considero que este hecho puede ser un próximo paso para el análisis de lo propuesto por los autores. Finalmente, otra opción a seguir también puede ser la perspectiva del análisis de la contabilidad de crecimiento en otros países de la región. De hecho, Vera Tudela (2013) explora un análisis similar durante 1960-2010; esto podría servir para contrastar el caso peruano con el de otros países de latinoamérica.
PARTE 2: Código en Python -#
Código hecho por Karen Arevalo y Mayeli Charra#
El Modelo Ingreso-Gasto: la Curva IS#
Utilizando las ecuaciones derive paso a paso la curva IS matemáticamente (a partir de la condición de equilibrio Y = DA).
El modelo Ingreso-Gasto muestra el equilibrio en el mercaso de biener entre el ingreso y la demanda agregada, partiendo por la condición de equilibrio Y=DA observamos que:
Donde:
Entonces:
De forma corta:
Donde \( α_0 = (C_0 + I_0 + G_0 + X_0 -hr)\) es el intercepto y \( α_1 = (b - m)(1 - t) \) es la pendiente de la función
Resolviendo, encontramos que:
O, igual que:
Usando la función de equilibrio IS donde r está en función de Y, encuentre \(Δr/ΔY\) que representa la pendiente y que signo tiene?
Función de equilibrio IS donde r está en función de Y:
conocemos que, la forma breve de esta ecuación es:
Donde: \(β_0=C_0+I_0+G_0+X_0\) y \(β_1=1-(b-m)(1-t)\)
Entonces, la pendiente de la curva IS va a ser MAYOR (>) que 0. Además va a poder ser representada gráficamente en el plano (Y,r) teniendo una recta con pendiente negativa:
import matplotlib.pyplot as plt
import numpy as np
import sympy as sy
import pandas as pd
from causalgraphicalmodels import CausalGraphicalModel
from sympy import *
Y, h, Co, Io, Go, Xo, b, m, t = symbols('Co Io Go Xo h r b m t')
r=(1/h)*(Co + Io + Go + Xo)-(1/h)*(1-(b-m)*(1-t))*Y
df_rY = diff(r, Y) #diff(función, variable_analizar
df_rY #Δr/ΔGY
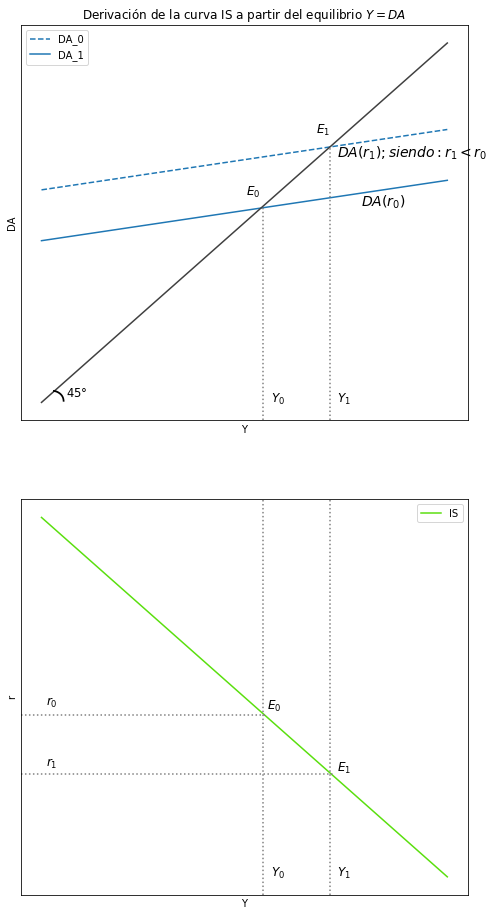
Lea la sección 4.4 del material de enseñanza y explique cómo se deriva la curva IS a partir del equilibrio Y=DA y grafique lo siguiente:
Partimos por la noción de equilibrio entre la Demanda Agregada y Y. Asimismo, se sabe que Y es la suma de la función de consumo más la inversión, el gasto del gobierno y las exportaciones, menos las importaciones.
Analizando cada uno de estos puntos, encontramos que:
La función de consumo es producto de la suma entre la variable del consumo autónomo más la variación (o propensión marginal a consumir) por Yd (el ingreso disponible).
La función de Inversión está dada por la resta entre la Inversión autónoma menos la propensión (o sensibilidad de los inversionistas en la tassa de interés) por r (real activo).
El gasto del gobierno será equivalente al gasto autónomo del gobierno.
Las exportacioes son equivalentes a las exportaciones autónomas
Las importaciones depende de la propensión marginal a importar.
Recordando ecuaciones:
\( C = C_0 + bY^d \)
\( I = I_0 - hr \)
\( G = G_0 \)
\( T = tY \)
\( X = X_0 \)
\( M = mY^d \)
Tenemos la siguiente condición de equilibrio:
Ecuación en función de r:
Ecuación en función de Y (relación inversa):
- Demanda Agregada:#
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
r = 0.9
Y = np.arange(Y_size)
# Ecuación de la curva del ingreso de equilibrio
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_IS_K = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y)
#--------------------------------------------------
# Recta de 45°
a = 2.5
def L_45(a, Y):
L_45 = a*Y
return L_45
L_45 = L_45(a, Y)
#--------------------------------------------------
# Segunda curva de ingreso de equilibrio
# Definir cualquier parámetro autónomo
Go = 35
# Generar la ecuación con el nuevo parámetro
def DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y):
DA_K = (Co + Io + Go + Xo - h*r) + ((b - m)*(1 - t)*Y)
return DA_K
DA_G = DA_K(Co, Io, Go, Xo, h, r, b, m, t, Y) # lista con 100 valores
- Curva IS#
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
Y = np.arange(Y_size)
# Ecuación
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
return r_IS
r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)
# Gráfico de la derivación de la curva IS a partir de la igualdad (DA = Y)
# Dos gráficos en un solo cuadro (ax1 para el primero y ax2 para el segundo)
fig, (ax1, ax2) = plt.subplots(2, figsize=(8, 16))
#---------------------------------
# Gráfico 1: ingreso de Equilibrio
ax1.yaxis.set_major_locator(plt.NullLocator())
ax1.xaxis.set_major_locator(plt.NullLocator())
ax1.plot(Y, DA_IS_K, label = "DA_0", linestyle = "dashed" , color = "C0")
ax1.plot(Y, DA_G, label = "DA_1", color = "C0")
ax1.plot(Y, L_45, color = "#404040")
ax1.axvline(x = 70.5, ymin= 0, ymax = 0.69, linestyle = ":", color = "grey")
ax1.axvline(x = 54, ymin= 0, ymax = 0.54, linestyle = ":", color = "grey")
ax1.text(6, 4, '$45°$', fontsize = 11.5, color = 'black')
ax1.text(2.5, -3, '$◝$', fontsize = 30, color = 'black')
ax1.text(72, 0, '$Y_1$', fontsize = 12, color = 'black')
ax1.text(56, 0, '$Y_0$', fontsize = 12, color = 'black')
ax1.text(67, 185, '$E_1$',fontsize = 12, color = 'black')
ax1.text(50, 142, '$E_0$', fontsize = 12, color = 'black')
#Anotaciones
ax1.text(72, 169, '$DA(r_1); siendo : r_1<r_0$',fontsize = 14, color = 'black')
ax1.text(78, 135, '$DA(r_0)$',fontsize = 14, color = 'black')
ax1.set(title = "Derivación de la curva IS a partir del equilibrio $Y=DA$", xlabel = r'Y', ylabel = r'DA')
ax1.legend()
#---------------------------------
# Gráfico 2: Curva IS
ax2.yaxis.set_major_locator(plt.NullLocator())
ax2.xaxis.set_major_locator(plt.NullLocator())
ax2.plot(Y, r, label = "IS", color = "#5ADF0E")
ax2.axvline(x = 70.5, ymin= 0, ymax = 1, linestyle = ":", color = "grey")
ax2.axvline(x = 54, ymin= 0, ymax = 1, linestyle = ":", color = "grey")
plt.axhline(y = 151.5, xmin= 0, xmax = 0.7, linestyle = ":", color = "grey")
plt.axhline(y = 165, xmin= 0, xmax = 0.55, linestyle = ":", color = "grey")
ax2.text(72, 128, '$Y_1$', fontsize = 12, color = 'black')
ax2.text(56, 128, '$Y_0$', fontsize=12, color = 'black')
ax2.text(1, 153, '$r_1$', fontsize = 12, color = 'black')
ax2.text(1, 167, '$r_0$', fontsize = 12 , color = 'black')
ax2.text(72, 152, '$E_1$', fontsize = 12 , color = 'black')
ax2.text(55, 166, '$E_0$', fontsize = 12, color = 'black')
ax2.set(title = "", xlabel = r'Y', ylabel = r'r')
ax2.legend()
plt.show()
La Curva IS o el equilibrio Ahorro- Inversión#
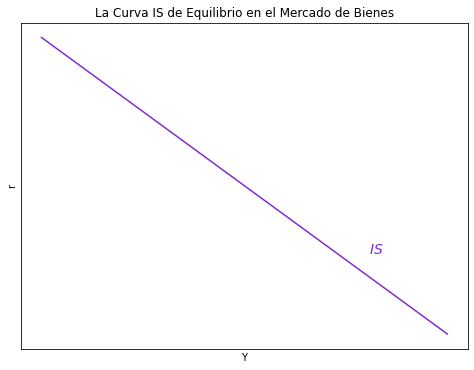
Derive la ecuación de IS a partir de la igualdad Ahorro-Inversión y grafique la curva IS de equilibrio en el Mercado de Bienes.
Se tiene que el equilibrio entre el ingreso y la demanda agregada (DA) son equivalentes al equilibrio que existe entre los valores del ahorro total y la inversión. En ese sentido, partiendo por la condición de equilibrio donde \(DA=Y\), obtenemos que:
Al resolver matemáticamente esto, llegamos al equilibrio entre Ahorro- Inversión. Así, restamos la tributación (dada por “T”) de ambas partes para encontrar la ecuación de ingreso disponible.
Dicha igualdad encontrada puede ser reescribida de la siguiente manera:
La parte derecha de la ecuación constituye el ahorro total el cual es equivalente al ingreso. El ahorro total incluirá el Ahorro Privado, el Ahorro del Gobierno y el Ahorro Externo.
Es esta igualdad entre el ahorro y la inversión, que constituyen la curva IS:
Reemplazando esto, encontramos que:
Y, mediante de operaciones algebraicas, obtenemos la ecuación de la Curva IS:
Con un par de operaciones más, la Curva IS encontrada puede expresarse a través de una ecuación en la que la tasa de interés esté en función del ingreso:
Esta relación encontrada, puede ser mostrada como:
Donde: \(β_0=C_0+I_0+G_0+X_0\) y \(β_1=1-(b-m)(1-t)\)
#Gráfico
z_size = 100
z = np.arange(z_size)
z
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
def funcion_2(x, z):
funcion_2 = (x - z)
return funcion_2
funcion_2(95, z)
array([95, 94, 93, 92, 91, 90, 89, 88, 87, 86, 85, 84, 83, 82, 81, 80, 79,
78, 77, 76, 75, 74, 73, 72, 71, 70, 69, 68, 67, 66, 65, 64, 63, 62,
61, 60, 59, 58, 57, 56, 55, 54, 53, 52, 51, 50, 49, 48, 47, 46, 45,
44, 43, 42, 41, 40, 39, 38, 37, 36, 35, 34, 33, 32, 31, 30, 29, 28,
27, 26, 25, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11,
10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3, -4])
f2 = funcion_2(95, z)
Z = np.arange(z_size)
a = -2.5
def L_45(a, Z):
L_45 = a*Z
return L_45
L_45 = L_45(a, Z)
y_max = np.max(L_45)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(Z, L_45, color = "#7E2CD0")
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
plt.text(80, -180, '$IS$', fontsize = 14, color = '#7E2CD0')
plt.title("La Curva IS de Equilibrio en el Mercado de Bienes")
plt.xlabel("Y")
plt.ylabel("r")
Text(0, 0.5, 'r')
Desequilibrios en el mercado de bienes#
Grafique las areas de exceso de oferta o exceso de demanda en el mercado de bienes. Explique por qué estos puntos están fuera de los puntos de equilibrio en el mercado de bienes.
#Equilibrio y Desequilibrio en el Mercado de Bienes
#Gráfico
z_size = 100
z = np.arange(z_size)
z
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
def funcion_3(x, z):
funcion_3 = (x - z)
return funcion_3
funcion_2(95, z)
array([95, 94, 93, 92, 91, 90, 89, 88, 87, 86, 85, 84, 83, 82, 81, 80, 79,
78, 77, 76, 75, 74, 73, 72, 71, 70, 69, 68, 67, 66, 65, 64, 63, 62,
61, 60, 59, 58, 57, 56, 55, 54, 53, 52, 51, 50, 49, 48, 47, 46, 45,
44, 43, 42, 41, 40, 39, 38, 37, 36, 35, 34, 33, 32, 31, 30, 29, 28,
27, 26, 25, 24, 23, 22, 21, 20, 19, 18, 17, 16, 15, 14, 13, 12, 11,
10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, -1, -2, -3, -4])
f3 = funcion_2(95, z)
Z = np.arange(z_size)
a = -2.5
def L_45(a, Z):
L_45 = a*Z
return L_45
L_45 = L_45(a, Z)
y_max = np.max(L_45)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(Z, L_45, color = "red")
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_locator(plt.NullLocator())
plt.text(90, -250, '$IS$', fontsize = 14, color = 'red')
plt.text(45, -105, '$A$', fontsize = 12, color = 'grey')
plt.text(60, -105, '$B$', fontsize = 12, color = 'grey')
plt.text(30, -105, '$C$', fontsize = 12, color = 'grey')
plt.text(-10, -105, '$rA$', fontsize = 12, color = 'grey')
plt.text(45, -280, '$YA$', fontsize = 12, color = 'grey')
plt.text(60, -280, '$YB$', fontsize = 12, color = 'grey')
plt.text(30, -280, '$YC$', fontsize = 12, color = 'grey')
# Lineas punteadas
plt.axvline(x = 60, ymin= 0, ymax = 0.56, linestyle = ":", color = "grey")
plt.axvline(x = 45, ymin= 0, ymax = 0.56, linestyle = ":", color = "grey")
plt.axvline(x = 30, ymin= 0, ymax = 0.56, linestyle = ":", color = "grey")
plt.axhline(y = -110, xmin= 0, xmax = 0.60, linestyle = ":", color = "grey")
#Texto: Exceso de demanda y Exceso de Oferta
plt.text(60, -60, '$Exceso$', fontsize = 12, color = 'black')
plt.text(60, -70, '$de$', fontsize = 12, color = 'black')
plt.text(60, -80, '$Oferta$', fontsize = 12, color = 'black')
plt.text(30, -180, '$Exceso$', fontsize = 12, color = 'black')
plt.text(30, -190, '$de$', fontsize = 12, color = 'black')
plt.text(30, -200, '$Demanda$', fontsize = 12, color = 'black')
plt.title("Equilibrio y Desequilibrio en el Mercado de Bienes")
plt.xlabel("Y")
plt.ylabel("r")
Text(0, 0.5, 'r')
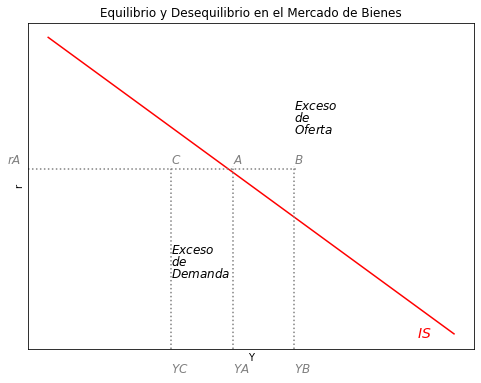
Sabemos que en el equilibrio de mercado de bienes, todos los puntos de la curva IS serán pares ordenados de \((Y,r)\). Consecuentemente, aquellos puntos que están fuera de esta curva, suponen el desequilibrio del mercado de bienes. Por lo que es importante que identifiquemos el tipo desequilibrio existente en el mercado (ya sea por exceso de la oferta o de la demanda).
En el gráfico realizado, se observa el punto A, dicho punto correspondería al punto \((YA, rA)\) el cual equilibraría el ahorro con la inversión; es decir, \(IA=SA\). Por otro lado, también se visualiza el punto B, cuyos pares ordenados corresponden a \((YB, rB)\). En este punto notamos que se encuentra a la derecha de la curva IS, mnteniendo la tasa de interés y la inversión permanece constante; sin embargo, el ahorro es mayor que el del punto A, pues los ingresos de B son mayores. Entonces, en el punto B, \(IA<SB\); situándose así, a la derecha de la IS, mostrando el desequilibrio del mercado de bienes por exceso de oferta.
De la misma forma, podemos notar que el punto C del lado izquierdo de la curva IS, mostraría el desequilibrio del mercado de bienes por exceso de demanda
Movimientos de la curva IS#
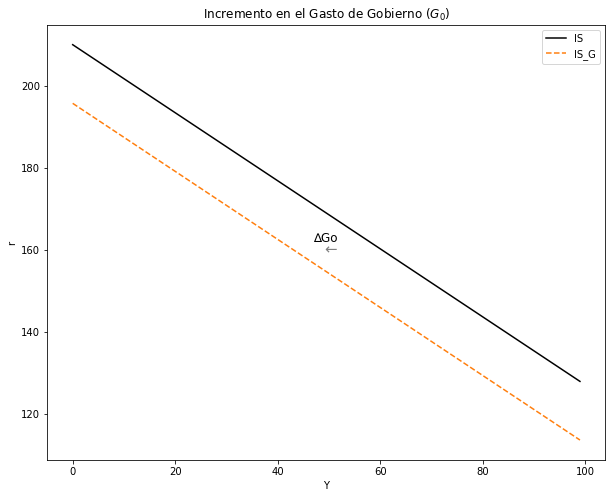
Analice una \(Política Fiscal Contractiva\) con caída del Gasto del Gobierno\(( △G<0)\) . El análisis debe ser intuitivo y gráfico.
- Intuición:#
Se intuye que al disminuir el gasto del gobierno, aumentará el ahorro. Consecuentemente, se producirá exceso de oferta de bienes. El movimiento de esta curva es hacia la izquierda.
- Graficamente:#
# Curva IS ORIGINAL
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.3
Y = np.arange(Y_size)
# Ecuación
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
return r_IS
r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)
#--------------------------------------------------
# NUEVA curva IS
# Definir SOLO el parámetro cambiado
Go = 60
# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
return r_IS
r_G = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "black") #IS orginal
ax.plot(Y, r_G, label = "IS_G", color = "C1", linestyle = 'dashed') #Nueva IS
# Texto agregado
plt.text(47, 162, '∆Go', fontsize=12, color='black')
plt.text(49, 159, '←', fontsize=15, color='grey')
# Título, ejes y leyenda
ax.set(title = "Incremento en el Gasto de Gobierno $(G_0)$", xlabel= 'Y', ylabel= 'r')
ax.legend()
plt.show()
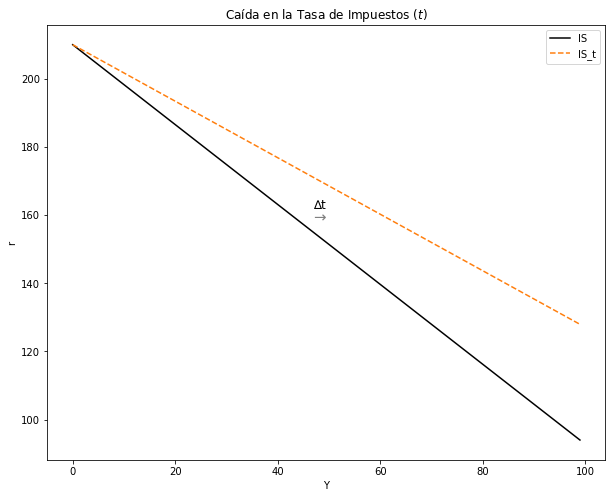
Analice una \(Política Fiscal Expansiva\) con una caída de la Tasa de Impuestos \(( △t<0)\) . El análisis debe ser intuitivo y gráfico.
- Intuición:#
Se tiene que si la tasa de impuestos cae hay aumento en las importaciones y en el consumo, disminuyendo el ahorro. La pendiente IS disminuirá.
- Graficamente:#
# Curva IS ORIGINAL
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.7
Y = np.arange(Y_size)
# Ecuación
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
return r_IS
r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)
#--------------------------------------------------
# NUEVA curva IS
# Definir SOLO el parámetro cambiado
t = 0.3
# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
return r_IS
r_t = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "black") #IS orginal
ax.plot(Y, r_t, label = "IS_t", color = "C1", linestyle = 'dashed') #Nueva IS
# Texto agregado
plt.text(47, 162, '∆t', fontsize=12, color='black')
plt.text(47, 158, '→', fontsize=15, color='grey')
# Título, ejes y leyenda
ax.set(title = "Caída en la Tasa de Impuestos $(t)$", xlabel= 'Y', ylabel= 'r')
ax.legend()
plt.show()
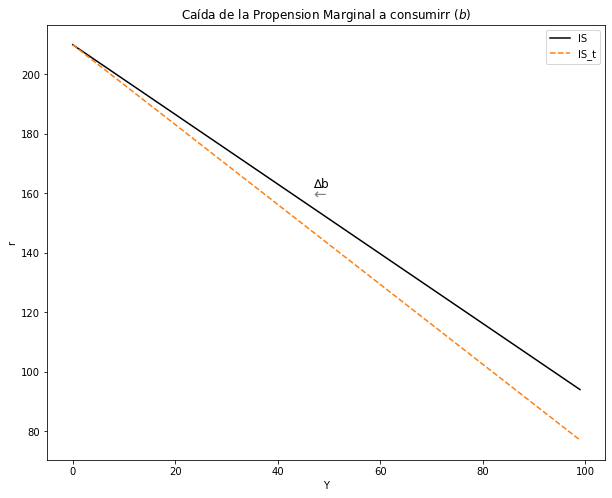
Analice una caída de la \(Propensión Marginal\) a Consumir \(( △b<0)\).El análisis debe ser intuitivo, matemático y gráfico.
- Intuitivamente#
Se tiene que si la propensión marginal cae, hay una reducción en la curva, pues cambia la pendiente hacia la izquierda. Se disminuye la demanda agregada y ocurre aumento del ahorro.
- Gráficamente#
#--------------------------------------------------
# Curva IS ORIGINAL
# Parámetros
Y_size = 100
Co = 35
Io = 40
Go = 70
Xo = 2
h = 0.7
b = 0.8
m = 0.2
t = 0.7
Y = np.arange(Y_size)
# Ecuación
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
return r_IS
r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)
#--------------------------------------------------
# NUEVA curva IS
# Definir SOLO el parámetro cambiado
b = 0.4
# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
return r_IS
r_b = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)
# Gráfico
# Dimensiones del gráfico
y_max = np.max(r)
fig, ax = plt.subplots(figsize=(10, 8))
# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "black") #IS orginal
ax.plot(Y, r_b, label = "IS_t", color = "C1", linestyle = 'dashed') #Nueva IS
# Texto agregado
plt.text(47, 162, '∆b', fontsize=12, color='black')
plt.text(47, 158, '←', fontsize=15, color='grey')
# Título, ejes y leyenda
ax.set(title = "Caída de la Propension Marginal a consumirr $(b)$", xlabel= 'Y', ylabel= 'r')
ax.legend()
plt.show()