Capítulo 4: El Modelo IS-LM#

PARTE 1: Lectura de Mendoza, W. (2015). Demanda y oferta agregada en presencia de politicas monetarias no convencionales#

Mendoza en su texto “Demanda y oferta agregada en presencia de políticas monetarias no convencionales” parte por mostrar el problemático escenario de la crisis monetaria en el periodo 2008-2009. En ese sentido, reconoce que antes de la crisis, el principal instrumento de la Reserva Federal (Fed) era la tasa de interés de referencia para los mercados de fondos federales. Sin embargo, después de la crisis, dicha tasa de interés se redujo hasta llegar casi a cero; por lo tanto se aplicaron dos instrumentos de política no convencionales. Por lo que el texto se guía a partir de la noción de ¿cómo afectará a la oferta y a la demanda la presencia de estos nuevos instrumentos no convencionales?

Para responder a esta cuestión, Mendoza presenta un nuevo modelo que sigue la tradición del modelo viejo keynesiano, siendo así una extensión del modelo IS-LM pero enriquecido con modelos de activos financieros. Esta esencia del trabajo de Mendoza representa una fortaleza, pues demuestra que los modelos antiguos pueden “reinventarse” para ser de utilidad a las problemáticas macroeconómicas actuales.

Siguiendo esta misma línea, Mendoza explora el primer instrumento de política no convencional: El anuncio sobre la trayectoria futura de la tasa de interés de corto plazo. A diferencia de otros modelos IS-LM, Fed administra la tasa de interés a corto plazo (más no la oferta monetaria). El segundo instrumento está dado por la intervención (compra) directa en el mercado de bonos a largo plazo (componente de la flexibilización cuantitativa). Para poder tratarla, se agrega un mercado de bonos a largo plazo en el modelo tradicional de IS-LM. Todo lo mencionado anteriormente, constituye parte de la demanda agregada de la economía, la cual se ve conjugado con una curva de oferta agregada para obtener un nuevo modelo macroeconómico.

Las características principales de este nuevo modelo, es que permite encontrar los valores de equilibrio de la producción, la tasa de interés a largo plazo y el nivel de precios. Asimismo, la principal fortaleza de este es que permite discutir los efectos sobre las Variables Endógenas del modelo convencional de política monetaria; así como, discutir sobre los efectos de política fiscal y choque adverso en la oferta.

Las fortalezas de esta propuesta y este enfoque son múltiples, elabora ejemplos, brinda ejercicios de estática comparativa (que simulan los efectos de las políticas macroeconómicas aplicadas a los 4 contextos: en el corto plazo, en el tránsito al equilibrio estacionario, en el equilibrio estacionario y los efectos con expectativas racionales). Sin embargo, una debilidad podría ser que si bien este documento se empeña por demostrar que los modelos antiguos pueden ser de utilidad, esto no significa que siempre sea así.

Mendoza concluye su investigación alegando entonces que, la inclusión de un mercado de bonos a largo plazo, en el modelo IS-LM permite discutir las cuestiones de política monetaria no convencionales de 2008-2009 de manera simplificada. Así mismo, del modelo IS-LM-BB, del que se desprende la demanda agregada de esta economía, se le agrega una ecuación de la oferta agregada, para construir un modelo que estudie los efectos de las políticas macroeconómicas.

Por otro lado, me gustaría hacer sugerencias que podrían potenciar más el trabajo de Mendoza. En primer lugar, si bien Mendoza se enfocó en estos dos instrumentos, sería interesante que introdujera otros elementos que usualmente son empleados en la política monetaria no convencional, y argumentar por qué no podrían haber funcionado efectivamente en el contexto de la crisis 2008-2009. Siguiendo lo planteado por Castillo y Contreras (2010), se podrían establecer comparaciones con otros instrumentos como: el programa de compras de activos, las operaciones estructurales o de ajuste, etc. De la misma manera, siguiendo la propuesta de Cano (2020) sería enriquecedor que, a partir de lo propuesto por Mendoza, se examine la política monetaria no convencional en la mitigación de los efectos económicos del COVID-19 en el país o en la región.

PARTE 2: Código en Python -#

Código hecho por Karen Arevalo y Mayeli Charra#

A partir del siguiente sistema de ecuaciones que representan el modelo IS-LM#

Encuentro con las ecuaciones de Ingreso (\( Y^e \)) y tasa de interés (\( r^e \)) de equilibrio (Escriba paso a paso la derivacion de estas ecuaciones).#

Por un lado, necesitamos considerar la ecuación de la curva IS

\[ r = \frac{B_o}{h} - \frac{B_1}{h}Y \]

  • En la cual \( B_0 = C_o + I_o + G_o + X_o \) y \( B_1 = 1 - (b - m)(1 - t) \)

Por otro lado, tenemos la ecuación de la curva LM:

\[ r = -\frac{1}{j}\frac{Mo^s}{P_o} + \frac{k}{j}Y \]

Al igual ambas ecuaciones, podemos encontrar el nivel de Ingresos equilibrio \((Y^e)\) y la tasa de interés de equilibrio \((r^e)\):

\[ -\frac{1}{j}\frac{Mo^s}{P_o} + \frac{k}{j}Y = \frac{B_o}{h} - \frac{B_1}{h}Y \]

  • Ingreso de equilibrio:

\[ Y^e = \frac{j B_o}{k h + j B_1} + (\frac{h}{k h + j B_1})\frac{Ms_o}{P_o} \]

  • Tasa de interés de equilibrio:

\[ r^e = \frac{kB_o}{kh + jB_1} - (\frac{B_1}{kh + jB_1})\frac{Ms_o}{P_o} \]

Estas dos ecuaciones representan el modelo IS-LM y los puntos o valores de equilibrio

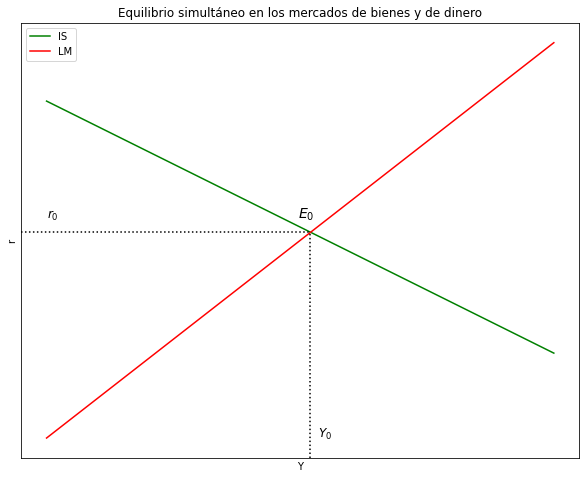
Grafique el equilibrio simultáneo en los mercados de bienes y de dinero.#

import matplotlib.pyplot as plt
import numpy as np
import sympy as sy
import pandas as pd
from sympy import *

# Curva IS

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo)/h - ( ( 1-(b-m)*(1-t) ) / h)*Y  
    return r_IS

r_is = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#--------------------------------------------------
    # Curva LM 

# Parámetros

Y_size = 100

k = 2
j = 1                
Ms = 200             
P  = 20               

Y = np.arange(Y_size)

# Ecuación

def r_LM(k, j, Ms, P, Y):
    r_LM = - (1/j)*(Ms/P) + (k/j)*Y
    return r_LM

r_lm = r_LM( k, j, Ms, P, Y)

# Gráfico del modelo IS-LM

# Dimensiones del gráfico
y_max = np.max(r_lm)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
# Curva IS
ax.plot(Y, r_is, label = "IS", color = "green") #IS
# Curva LM
ax.plot(Y, r_lm, label="LM", color = "red")  #LM

# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())   
ax.xaxis.set_major_locator(plt.NullLocator())

# Texto y figuras agregadas
# Graficar la linea horizontal - r
plt.axvline(x=51.5,  ymin= 0, ymax= 0.52, linestyle = ":", color = "black")
# Grafica la linea vertical - Y
plt.axhline(y=93, xmin= 0, xmax= 0.52, linestyle = ":", color = "black")

# Plotear los textos 
plt.text(49,100, '$E_0$', fontsize = 14, color = 'black')
plt.text(0,100, '$r_0$', fontsize = 12, color = 'black')
plt.text(53,-10, '$Y_0$', fontsize = 12, color = 'black')

# Título, ejes y leyenda
ax.set(title="Equilibrio simultáneo en los mercados de bienes y de dinero", xlabel= r'Y', ylabel= r'r')
ax.legend()

plt.show()
_images/Reporte4_8_0.png

Estática comparativa#

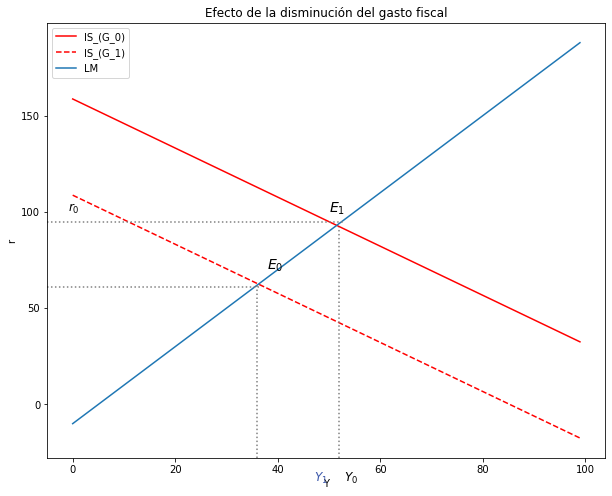
Analice los efectos sobre las variables endógenas Y, r de una disminución del gasto fiscal. (\(ΔG_0<0\)). El análisis debe ser intuitivo, matemático y gráfico.#

  • Intuitivamente:

\(G↓→DA↓→DA > Y→Y↓\) (\(Y\) es la variable de ajuste) <–> \(DA=Y\) (Mercado de bienes)

\(Y↓→Md↓→Md > Ms→r↓\) (\(r\) es la variable de ajuste) <–> \(M^d=M^s\) (Mercado monetario)

  • Matemáticamente:

\[ ΔY^e = \frac{j}{k h + j B_1} * ΔG_0 > 0 \]
\[ Δr^e = \frac{k}{kh + jB_1} * ΔG_0 > 0 \]

  • Gráficamente:

# Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#2--------------------------------------------------
    # Curva LM ORIGINAL

# Parámetros

Y_size = 100

k = 2
j = 1                
Ms = 200             
P  = 20               

Y = np.arange(Y_size)

# Ecuación

def i_LM( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i = i_LM( k, j, Ms, P, Y)

# NUEVA curva IS: reducción Gasto Fiscal de Gobienro (Go)
    
# Definir parámetro cambiado
Go = 10

# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_G = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

# Gráfico

# Dimensiones del gráfico
y_max = np.max(i)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS_(G_0)", color = "red") #IS_orginal
ax.plot(Y, r_G, label = "IS_(G_1)", color = "red", linestyle = 'dashed') #IS_modificada

ax.plot(Y, i, label="LM", color = "C0")  #LM_original

# Texto y figuras agregadas
plt.axvline(x=36,  ymin= 0, ymax= 0.40, linestyle = ":", color = "grey")
plt.axhline(y=61, xmin= 0, xmax= 0.38, linestyle = ":", color = "grey")

plt.axvline(x=52,  ymin= 0, ymax= 0.53, linestyle = ":", color = "grey")
plt.axhline(y=95, xmin= 0, xmax= 0.53, linestyle = ":", color = "grey")
plt.text(50,100, '$E_1$', fontsize = 14, color = 'black')

plt.text(38,70, '$E_0$', fontsize = 14, color = 'black')
plt.text(-1,100, '$r_0$', fontsize = 12, color = 'black')
plt.text(53,-40, '$Y_0$', fontsize = 12, color = 'black')
#plt.text(50,52, '$E_1$', fontsize = 14, color = '#3D59AB')
#plt.text(-1,72, '$r_1$', fontsize = 12, color = '#3D59AB')
plt.text(47,-40, '$Y_1$', fontsize = 12, color = '#3D59AB')

#plt.text(69, 115, '→', fontsize=15, color='grey')
#plt.text(69, 52, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title="Efecto de la disminución del gasto fiscal", xlabel= r'Y', ylabel= r'r')
ax.legend()

plt.show()
_images/Reporte4_15_0.png

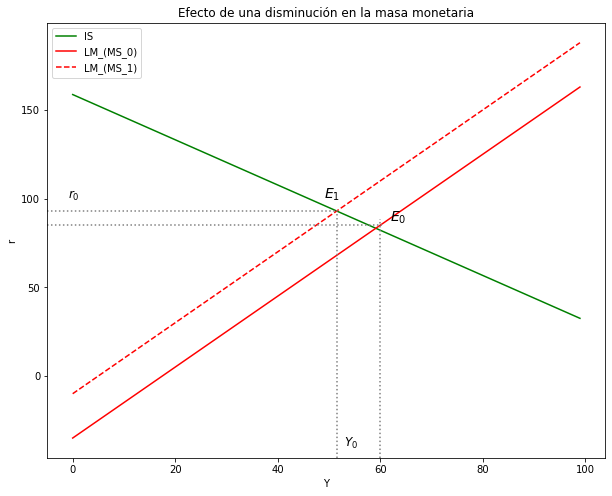
Analice los efectos sobre las variables endógenas Y, r de una disminución de la masa monetaria. (\(ΔM^s<0\)). El análisis debe ser intuitivo, matemático y gráfico.#

  • Intuitivamente:

\[ M^s_o ↓→Ms > Md→r↑ \]
\[ r↑→I↓→ DA > Y→Y↓ \]

  • Matemáticamente:

\[ ΔY^e = \frac{h}{k h + j B_1}\frac{1}{P} * ΔM^S_o < 0 \]
\[ Δr^e = \frac{B_1}{kh + jP_1}\frac{1}{P} * ΔM^S_o > 0 \]

  • Gráficamente:

# Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


# Curva LM ORIGINAL

# Parámetros

Y_size = 100

k = 2
j = 1                
Ms = 700             
P  = 20               

Y = np.arange(Y_size)

# Ecuación

def i_LM( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i = i_LM( k, j, Ms, P, Y)

# Definir el parámetro cambiado
Ms = 200

# Generar nueva curva LM con la variacion del Ms
def i_LM_Ms( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i_Ms = i_LM_Ms( k, j, Ms, P, Y)

# Gráfico

# Dimensiones del gráfico
y_max = np.max(i)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "green") #IS_orginal
ax.plot(Y, i, label="LM_(MS_0)", color = "red")  #LM_original

ax.plot(Y, i_Ms, label="LM_(MS_1)", color = "red", linestyle = 'dashed')  #LM_modificada

# Lineas de equilibrio_0 
plt.axvline(x=51.5,  ymin= 0, ymax= 0.57, linestyle = ":", color = "grey")
plt.axhline(y=93, xmin= 0, xmax= 0.52, linestyle = ":", color = "grey")

# Lineas de equilibrio_1 
plt.axvline(x=60,  ymin= 0, ymax= 0.55, linestyle = ":", color = "grey")
plt.axhline(y=85, xmin= 0, xmax= 0.6, linestyle = ":", color = "grey")
plt.text(62,87, '$E_0$', fontsize = 14, color = 'black')

#plt.axhline(y=68, xmin= 0, xmax= 0.52, linestyle = ":", color = "grey")

# Textos ploteados
plt.text(49,100, '$E_1$', fontsize = 14, color = 'black')
plt.text(-1,100, '$r_0$', fontsize = 12, color = 'black')
plt.text(53,-40, '$Y_0$', fontsize = 12, color = 'black')
#plt.text(50,52, '$E_1$', fontsize = 14, color = '#3D59AB')
#plt.text(-1,72, '$r_1$', fontsize = 12, color = '#3D59AB')
#plt.text(47,-40, '$Y_1$', fontsize = 12, color = '#3D59AB')

#plt.text(69, 115, '→', fontsize=15, color='grey')
#plt.text(69, 52, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title="Efecto de una disminución en la masa monetaria", xlabel= r'Y', ylabel= r'r')
ax.legend()

plt.show()
_images/Reporte4_22_0.png

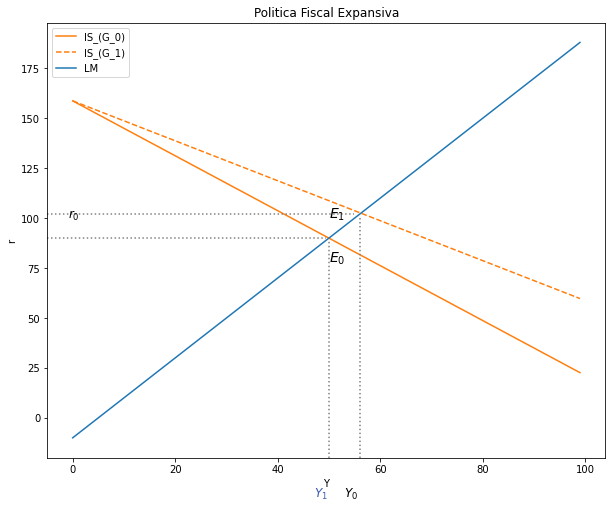
Analice los efectos sobre las variables endógenas Y, r de un incremento de la tasa de impuestos (\(ΔM^s<0\)). El análisis debe ser intuitivo, matemático y gráfico.#

  • Intuitivamente:

  • Mercado de Bienes $\( t↑ → DA↓ → DA < Y → Y↓ \)$

  • Mercado de dinero $\( Y↓ → Md↓ → Md<Ms → r↓ \)$

  • Matemáticamente: $\( ΔY^e = \frac{j}{k h + j B_1} * Δt < 0 \)$

\[ Δr^e = \frac{k}{kh + jB_1} * Δt < 0 \]

  • Gráficamente:

#1--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.001

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#2--------------------------------------------------
    # Curva LM ORIGINAL

# Parámetros

Y_size = 100

k = 2
j = 1                
Ms = 200             
P  = 20               

Y = np.arange(Y_size)

# Ecuación

def i_LM( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i = i_LM( k, j, Ms, P, Y)

#--------------------------------------------------
    # NUEVA curva IS: incremento de la tasa de impuestos (t)
    
# Definir SOLO el parámetro cambiado
t = 3

# Generar la ecuación con el nuevo parámetro
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r_G = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)

# Gráfico

# Dimensiones del gráfico
y_max = np.max(i)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS_(G_0)", color = "C1") #IS_orginal
ax.plot(Y, r_G, label = "IS_(G_1)", color = "C1", linestyle = 'dashed') #IS_modificada

ax.plot(Y, i, label="LM", color = "C0")  #LM_original

# Texto y figuras agregadas
plt.axvline(x=50,  ymin= 0, ymax= 0.50, linestyle = ":", color = "grey")
plt.axhline(y=90, xmin= 0, xmax= 0.50, linestyle = ":", color = "grey")

plt.axvline(x=56,  ymin= 0, ymax= 0.55, linestyle = ":", color = "grey")
plt.axhline(y=102, xmin= 0, xmax= 0.55, linestyle = ":", color = "grey")
plt.text(50,100, '$E_1$', fontsize = 14, color = 'black')

plt.text(50,78, '$E_0$', fontsize = 14, color = 'black')
plt.text(-1,100, '$r_0$', fontsize = 12, color = 'black')
plt.text(53,-40, '$Y_0$', fontsize = 12, color = 'black')
plt.text(47,-40, '$Y_1$', fontsize = 12, color = '#3D59AB')

#plt.text(69, 115, '→', fontsize=15, color='grey')
#plt.text(69, 52, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title="Politica Fiscal Expansiva", xlabel= r'Y', ylabel= r'r')
ax.legend()

plt.show()
_images/Reporte4_29_0.png

Código (Tres puntos Extra!)#

A partir del siguiente sistema de ecuaciones que representan el modelo IS-LM#

1. Encuentro con las ecuaciones de Ingreso (\( Y^e \)) y tasa de interés (\( r^e \)) de equilibrio (Escriba paso a paso la derivacion de estas ecuaciones).#

Teniendo la tasa de interes nominal donde: $\( i = r+π^e \)$

  • Mercado de Bienes IS $\( [1-(b-m)(1-t)]Y - (C_0+G_0+x_0) = I_0 - h(r+π^e) \)$

\[ hi = [I_0+C_0+G_0+x_0]-[1-(b-m)(1-t)] \]
\[ i= \frac{1}{h} (I_0+C_0+G_0+x_0) - [\frac{1-(b-m)(1-t)}{h} ] Y\]

Donde: \( B_0 \) es \( I_0+C_0+G_0+x_0 \) y \( B_1\) es \( 1-(b-m)(1-t) \)

  • Mercado de dinero LM $\( M^d = M^s \)$

\[ kY-j(r+π^e) = \frac{Mo^s}{P_o} \]
\[ kY-\frac{Mo^s}{P_o} =ji \]
\[ kY-\frac{Mo^s}{P_o} =ji \]
\[ \frac{kY}{j}-\frac{Mo^s}{P_o} = i \]

\( Obtenemos: \)

\[ i = -\frac{Mo^s}{P_o}+ \frac{kY}{j}\]

  • Al igualar ambas ecuaciones tenemos: $\( -\frac{1}{j}\frac{Mo^s}{P_o} + \frac{k}{j}Y = \frac{B_o}{h} - \frac{B_1}{h}Y \)$

\(Finalmente: \)

  • Ingreso de equilibrio:

\[ Y^e = \frac{j B_o}{k h + j B_1} + (\frac{h}{k h + j B_1})\frac{Ms_o}{P_o} \]

  • Tasa de interés de equilibrio:

\[ r^e = \frac{kB_o}{kh + jB_1} - (\frac{B_1}{kh + jB_1})\frac{Ms_o}{P_o} \]

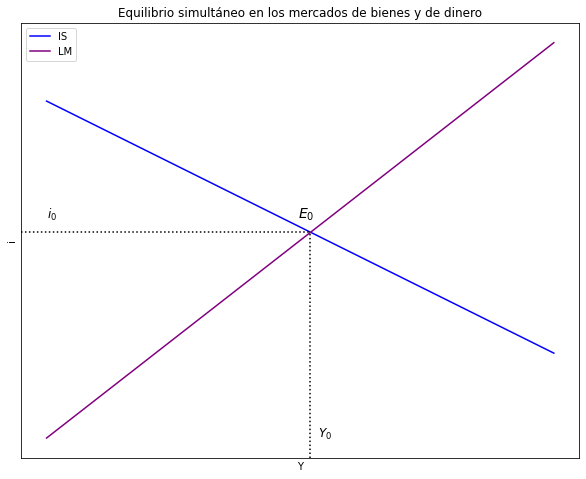
2. Grafique el equilibrio simultáneo en los mercados de bienes y de dinero.#

# Curva IS

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

Y = np.arange(Y_size)


# Ecuación 
def i_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    i_IS = (Co + Io + Go + Xo)/h - ( ( 1-(b-m)*(1-t) ) / h)*Y  
    return i_IS

i_is = i_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#--------------------------------------------------
    # Curva LM 

# Parámetros

Y_size = 100

k = 2
j = 1                
Ms = 200             
P  = 20               

Y = np.arange(Y_size)

# Ecuación

def i_LM(k, j, Ms, P, Y):
    i_LM = - (1/j)*(Ms/P) + (k/j)*Y
    return i_LM

i_lm = i_LM( k, j, Ms, P, Y)

# Gráfico del modelo IS-LM

# Dimensiones del gráfico
y_max = np.max(i_lm)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
# Curva IS
ax.plot(Y, i_is, label = "IS", color = "blue") #IS
# Curva LM
ax.plot(Y, i_lm, label="LM", color = "purple")  #LM

# Eliminar las cantidades de los ejes
ax.yaxis.set_major_locator(plt.NullLocator())   
ax.xaxis.set_major_locator(plt.NullLocator())

# Texto y figuras agregadas
# Graficar la linea horizontal - r
plt.axvline(x=51.5,  ymin= 0, ymax= 0.52, linestyle = ":", color = "black")
# Grafica la linea vertical - Y
plt.axhline(y=93, xmin= 0, xmax= 0.52, linestyle = ":", color = "black")

# Plotear los textos 
plt.text(49,100, '$E_0$', fontsize = 14, color = 'black')
plt.text(0,100, '$i_0$', fontsize = 12, color = 'black')
plt.text(53,-10, '$Y_0$', fontsize = 12, color = 'black')

# Título, ejes y leyenda
ax.set(title="Equilibrio simultáneo en los mercados de bienes y de dinero", xlabel= r'Y', ylabel= r'i')
ax.legend()

plt.show()
_images/Reporte4_35_0.png

Estática comparativa#

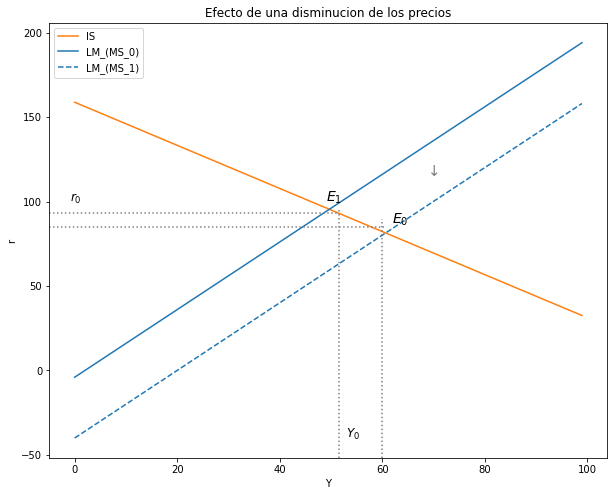
1. Analice los efectos sobre las variables endógenas Y, r de una disminución de los Precios (\(ΔP_0<0\)). El análisis debe ser intuitivo, matemático y gráfico.#

  • Intuitivamente:

\[ P_0↓ → M^s_o↑ →Ms > Md→r↑ \]
\[ r↑ → I↓ → DA > Y → Y↓ \]

  • Matemáticamente:

\[ \frac{ΔY}{ΔP_0} = \frac{h}{|A|P_0^2} >0 \]
\[ \frac{Δr}{ΔP_0} = \frac{hM_0^s[1-b(1-t)]}{|A|P_0^2} <0 \]

  • Gráficamente:

#1--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#2--------------------------------------------------
    # Curva LM ORIGINAL

# Parámetros

Y_size = 100

k = 2
j = 1                
Ms = 200             
P  = 50             

Y = np.arange(Y_size)

# Ecuación

def i_LM( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i = i_LM( k, j, Ms, P, Y)

# Definir SOLO el parámetro cambiado
P = 5

# Generar nueva curva LM con la variacion del Ms
def i_LM_Ms( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i_Ms = i_LM_Ms( k, j, Ms, P, Y)

# Gráfico

# Dimensiones del gráfico
y_max = np.max(i)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "C1") #IS_orginal
ax.plot(Y, i, label="LM_(MS_0)", color = "C0")  #LM_original

ax.plot(Y, i_Ms, label="LM_(MS_1)", color = "C0", linestyle = 'dashed')  #LM_modificada

# Lineas de equilibrio_0 
plt.axvline(x=51.5,  ymin= 0, ymax= 0.57, linestyle = ":", color = "grey")
plt.axhline(y=93, xmin= 0, xmax= 0.52, linestyle = ":", color = "grey")

# Lineas de equilibrio_1 
plt.axvline(x=60,  ymin= 0, ymax= 0.55, linestyle = ":", color = "grey")
plt.axhline(y=85, xmin= 0, xmax= 0.6, linestyle = ":", color = "grey")
plt.text(62,87, '$E_0$', fontsize = 14, color = 'black')

#plt.axhline(y=68, xmin= 0, xmax= 0.52, linestyle = ":", color = "grey")

# Textos ploteados
plt.text(49,100, '$E_1$', fontsize = 14, color = 'black')
plt.text(-1,100, '$r_0$', fontsize = 12, color = 'black')
plt.text(53,-40, '$Y_0$', fontsize = 12, color = 'black')
#plt.text(50,52, '$E_1$', fontsize = 14, color = '#3D59AB')
#plt.text(-1,72, '$r_1$', fontsize = 12, color = '#3D59AB')
#plt.text(47,-40, '$Y_1$', fontsize = 12, color = '#3D59AB')

plt.text(69, 115, '↓', fontsize=15, color='grey')
#plt.text(69, 52, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title="Efecto de una disminucion de los precios", xlabel= r'Y', ylabel= r'r')
ax.legend()

plt.show()
_images/Reporte4_42_0.png

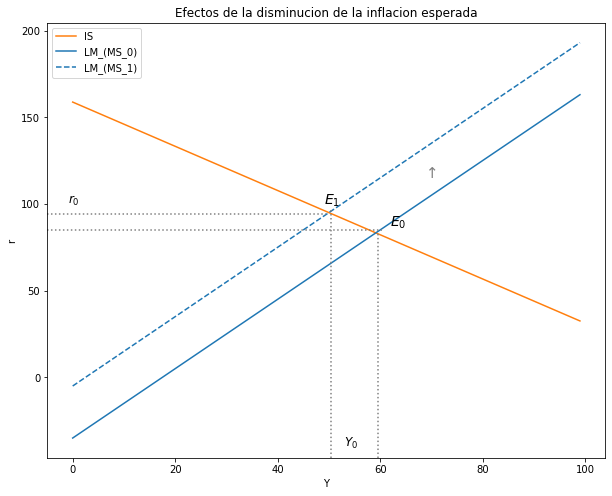
2. Analice los efectos sobre las variables endógenas Y, r de una disminución de la expansión esperada (\(Δπ<0\)) . El análisis debe ser intuitivo, matemático y gráfico.#

  • Intuitivamente:

\[ π↓ → i↓ M^d↑ →M^d > M^s →r↑ \]
\[ r↑→I↓→ DA < Y→Y↓ \]

  • Matemáticamente:

\[ \frac{ΔY}{Δπ^e} = \frac{jh}{|A|} < 0 \]
\[ \frac{Δr}{Δπ^e} = \frac{hM_0^s[-j[1-b(1-t)]}{|A|} > 0 \]

  • Graficamente:

#1--------------------------------------------------
    # Curva IS ORIGINAL

# Parámetros

Y_size = 100 

Co = 35
Io = 40
Go = 50
Xo = 2
h = 0.8
b = 0.4
m = 0.5
t = 0.8

Y = np.arange(Y_size)


# Ecuación 
def r_IS(b, m, t, Co, Io, Go, Xo, h, Y):
    r_IS = (Co + Io + Go + Xo - Y * (1-(b-m)*(1-t)))/h
    return r_IS

r = r_IS(b, m, t, Co, Io, Go, Xo, h, Y)


#2--------------------------------------------------
    # Curva LM ORIGINAL

# Parámetros

Y_size = 100

k = 2
j = 1 
Ms = 700   
P  = 20             

Y = np.arange(Y_size)

# Ecuación

def i_LM( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i = i_LM( k, j, Ms, P, Y)

# Definir SOLO el parámetro cambiado
Ms = 100

# Generar nueva curva LM con la variacion del Ms
def i_LM_Ms( k, j, Ms, P, Y):
    i_LM = (-Ms/P)/j + k/j*Y
    return i_LM

i_Ms = i_LM_Ms( k, j, Ms, P, Y)

# Gráfico

# Dimensiones del gráfico
y_max = np.max(i)
fig, ax = plt.subplots(figsize=(10, 8))

# Curvas a graficar
ax.plot(Y, r, label = "IS", color = "C1") #IS_orginal
ax.plot(Y, i, label="LM_(MS_0)", color = "C0")  #LM_original

ax.plot(Y, i_Ms, label="LM_(MS_1)", color = "C0", linestyle = 'dashed')  #LM_modificada

# Lineas de equilibrio_0 
plt.axvline(x=50.5,  ymin= 0, ymax= 0.57, linestyle = ":", color = "grey")
plt.axhline(y=94, xmin= 0, xmax= 0.50, linestyle = ":", color = "grey")

# Lineas de equilibrio_1 
plt.axvline(x=59.5,  ymin= 0, ymax= 0.52, linestyle = ":", color = "grey")
plt.axhline(y=85, xmin= 0, xmax= 0.6, linestyle = ":", color = "grey")
plt.text(62,87, '$E_0$', fontsize = 14, color = 'black')

#plt.axhline(y=68, xmin= 0, xmax= 0.52, linestyle = ":", color = "grey")

# Textos ploteados
plt.text(49,100, '$E_1$', fontsize = 14, color = 'black')
plt.text(-1,100, '$r_0$', fontsize = 12, color = 'black')
plt.text(53,-40, '$Y_0$', fontsize = 12, color = 'black')
#plt.text(50,52, '$E_1$', fontsize = 14, color = '#3D59AB')
#plt.text(-1,72, '$r_1$', fontsize = 12, color = '#3D59AB')
#plt.text(47,-40, '$Y_1$', fontsize = 12, color = '#3D59AB')

plt.text(69, 115, '↑', fontsize=15, color='grey')
#plt.text(69, 52, '←', fontsize=15, color='grey')

# Título, ejes y leyenda
ax.set(title="Efectos de la disminucion de la inflacion esperada", xlabel= r'Y', ylabel= r'r')
ax.legend()

plt.show()
_images/Reporte4_48_0.png